题目内容
【题目】物联网兴起、发展、完善极大的方便了市民生活需求.某市统计局随机地调查了该市某社区的100名市民网上购菜状况,其数据如下:
每周网上买菜次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 总计 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周网上买菜次数超过3次的用户称为“网上买菜热爱者”,能否在犯错误概率不超过0.005的前提下,认为是否为“网上买菜热爱者”与性别有关?
(2)把每周使用移动支付6次及6次以上的用户称为“网上买菜达人”,视频率为概率,在我市所有“网上买菜达人”中,随机抽取4名用户求既有男“网上买菜达人”又有女“网上买菜达人”的概率.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)在犯错误概率不超过0.005的前提下,能认为是否为“网上买菜热爱者”与性别有关(2)![]()
【解析】
(1)根据题意列出![]() 列联表,由公式计算
列联表,由公式计算![]() ,再由给出的对照表进行比较,得出结论.
,再由给出的对照表进行比较,得出结论.
(2)由题意可得随机抽取1名用户,该用户为男“移动支付达人”的概率为![]() ,女移动支付达人“的概率为
,女移动支付达人“的概率为![]() ,然后求出抽取的4名用户中,全为男“移动支付达人”的概率和抽取的4名用户中,全为女“移动支付达人”的概率,再由对立事件的概率可求出答案.
,然后求出抽取的4名用户中,全为男“移动支付达人”的概率和抽取的4名用户中,全为女“移动支付达人”的概率,再由对立事件的概率可求出答案.
(1)由表格数据可得![]() 列联表如下:
列联表如下:
非移动支付活跃用户 | 移动支付活跃用户 | 合计 | |
男 | 25 | 20 | 45 |
女 | 15 | 40 | 55 |
合计 | 40 | 60 | 100 |
将列联表中的数据代入公式计算得:
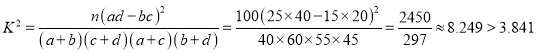 ,
,
所以在犯错误概率不超过0.005的前提下,能认为是否为“网上买菜热爱者”与性别有关.
(2)每周使用移动支付6次及6次以上的用户有45户.其中男性15户,女性30户.
视频率为概率,在我市“移动支付达人”中,随机抽取1名用户,
该用户为男“移动支付达人”的概率为![]() ,女移动支付达人“的概率为
,女移动支付达人“的概率为![]() .
.
抽取的4名用户中,全为男“移动支付达人”的概率为:![]()
抽取的4名用户中,全为女“移动支付达人”的概率为:![]()
抽取的4名用户中,既有男“移动支付达人”,又有女“移动支付达人”的概率为 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】从2016年到2019年的某城市方便面销量情况如图所示:
年份 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 1 | 2 | 3 | 4 |
年销量 | 462 | 444 | 404 | 385 |
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2020年(
.用所求回归方程预测2020年(![]() )方便面在该城市的年销量;
)方便面在该城市的年销量;
(2)某媒体记者随机对身边的10位朋友做了一次调查,其中3位受访者认为方便面是健康食品.现从这10人中抽取3人进行深度访谈,记![]() 表示随机抽取的3人认为方便面是健康食品的人数,求随机变量
表示随机抽取的3人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中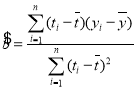 ,
,![]() .
.
参考数据:![]() .
.