题目内容
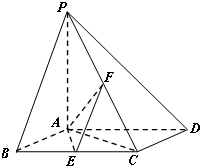 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为
| ||
| 2 |
分析:(I)根据题意可得:△ABC为正三角形,所以AE⊥BC,又因为BC∥AD,所以AE⊥AD.又PA⊥AE,且PA∩AD=A,所以AE⊥平面PAD,进而可得答案.
(II)建立坐标系,利用题中的已知条件分别求出两个平面的法向量,借助于向量的有关运算计算出向量的夹角,再转化为二面角的平面角.
(II)建立坐标系,利用题中的已知条件分别求出两个平面的法向量,借助于向量的有关运算计算出向量的夹角,再转化为二面角的平面角.
解答: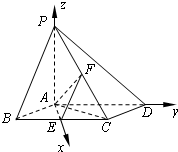 解:(Ⅰ)垂直.
解:(Ⅰ)垂直.
证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又因为BC∥AD,
所以AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
所以AE⊥平面PAD.
又PD?平面PAD,
所以AE⊥PD.
(Ⅱ)由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,
又E,F分别为BC,PC的中点,设AB=BC=CD=DA=2,所以AE=
,
AH⊥PD于H,此时EH与平面PAD所成最大角的正切值为
,
所以AH=
,sin∠PDA=
,
PA=DA=2,
∴A(0,0,0),B(
,-1,0),C(
,1,0),D(0,2,0),P(0,0,2),E(
,0,0),F(
,
,1),
所以
=(
,0,0),
=(
,
,1).
设平面AEF的一法向量为
=(x1,y1,z1),
则
因此
取z1=-1,
则
=(0,2,-1),因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故
为平面AFC的一法向量.
又
=(-
,3,0),所以cos<
,
>=
=
=
.
因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
.
 解:(Ⅰ)垂直.
解:(Ⅰ)垂直.证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又因为BC∥AD,
所以AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
所以AE⊥平面PAD.
又PD?平面PAD,
所以AE⊥PD.
(Ⅱ)由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,
又E,F分别为BC,PC的中点,设AB=BC=CD=DA=2,所以AE=
| 3 |
AH⊥PD于H,此时EH与平面PAD所成最大角的正切值为
| ||
| 2 |
所以AH=
| 2 |
| ||
| 2 |
PA=DA=2,
∴A(0,0,0),B(
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
所以
| AE |
| 3 |
| AF |
| ||
| 2 |
| 1 |
| 2 |
设平面AEF的一法向量为
| m |
则
|
|
则
| m |
| BD |
又
| BD |
| 3 |
| m |
| BD |
| ||||
|
|
| 2×3 | ||||
|
| ||
| 5 |
因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
| ||
| 5 |
点评:解决此类问题的关键是熟练掌握几何体的结构特征,以便利用已知条件得到空间的线面关系,并且便于建立坐标系利用向量的有关运算解决空间角等问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,