题目内容
【题目】已知椭圆C1 , 抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上各取两个点,其坐标分别是(3,一2 ![]() ),(一2,0),(4,一4),(
),(一2,0),(4,一4),( ![]() ). (Ⅰ)求C1 , C2的标准方程;
). (Ⅰ)求C1 , C2的标准方程;
(Ⅱ)是否存在直线L满足条件:①过C2的焦点F;②与C1交与不同的两点M,N且满足 ![]() ?若存在,求出直线方程;若不存在,说明理由.
?若存在,求出直线方程;若不存在,说明理由.
【答案】解:(Ⅰ)设抛物线C2:y2=2px(p≠0),
则有 ![]() ,x≠0,
,x≠0,
据此验证4个点知(3,﹣2 ![]() ),(4,﹣4)在抛物线上,
),(4,﹣4)在抛物线上,
∴C2:y2=4x,
设C1: ![]() ,(a>b>0),
,(a>b>0),
把点(﹣2,0),( ![]() ,
, ![]() )代入,得:
)代入,得:
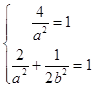 ,解得
,解得 ![]() ,
,
∴ ![]() 的方程为:
的方程为: ![]() .
.
(Ⅱ)当直线l的斜率不存在时,
直线l的方程为x=1,直线l交抛物线于M(1, ![]() ),N(1,﹣
),N(1,﹣ ![]() ),
),
![]() ≠0,不满足题意,
≠0,不满足题意,
当直线l的斜率存在时,假设存在直线l,过抛物线焦点F(1,0),
设其方程为y=k(x﹣1),与C1的交点坐标为M(x1,y1),N(x2,y2),
由 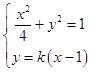 ,消去y并整理,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,
,消去y并整理,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,
∴ ![]() ,
, ![]() ,①
,①
y1y2=k(x1﹣1)k(x2﹣1)=k2[x1x2﹣(x1+x2)+1],
∴  =﹣
=﹣ ![]() ,②
,②
由 ![]() ,即
,即 ![]() =0,得x1x2+y1y2=0,
=0,得x1x2+y1y2=0,
将①,②代入(*)式,得 ![]() =
= ![]() ,
,
解得k=±2,
∴存在直线l满足条件,且l的方程为2x﹣y﹣2=0或2x+y﹣2=0
【解析】(Ⅰ)设抛物线C2:y2=2px(p≠0),则有 ![]() ,≠0,由此能求出C2:y2=4x,设C1:
,≠0,由此能求出C2:y2=4x,设C1: ![]() ,(a>b>0),由题意得
,(a>b>0),由题意得 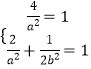 ,由此能求出
,由此能求出 ![]() 的方程为:
的方程为: ![]() .(Ⅱ)当直线l的斜率不存在时,直线l的方程为x=1,直线l交抛物线于M(1,
.(Ⅱ)当直线l的斜率不存在时,直线l的方程为x=1,直线l交抛物线于M(1, ![]() ),N(1,﹣
),N(1,﹣ ![]() ),
), ![]() ≠0,不满足题意,当直线l的斜率存在时,假设存在直线l,过抛物线焦点F(1,0),设其方程为y=k(x﹣1),与C1的交点坐标为M(x1,y1),N(x2,y2),由
≠0,不满足题意,当直线l的斜率存在时,假设存在直线l,过抛物线焦点F(1,0),设其方程为y=k(x﹣1),与C1的交点坐标为M(x1,y1),N(x2,y2),由 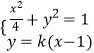 ,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,由此利用韦达定理结合已知条件能求出直线l的方程.
,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,由此利用韦达定理结合已知条件能求出直线l的方程.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】某同学用“五点法”画函数![]()
![]() 在某一周期内的图象时,列表并填入了部分数据,如下表:
在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(Ⅰ)请将上表数据补充完整,函数![]() 的解析式
的解析式![]() (直接写出结果即可)
(直接写出结果即可)
(Ⅱ)求函数![]() 的单调递增区间;/span>
的单调递增区间;/span>
(Ⅲ)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下: 表1:男生表2:女生
等级 | 优秀 | 合格 | 尚待改进 | 等级 | 优秀 | 合格 | 尚待改进 | |
频数 | 15 | x | 5 | 频数 | 15 | 3 | y |
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考数据与公式:
K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2>k0) | 0.05 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
