题目内容
在8×8棋盘的64个方格中,共有由整数个小方格组成的大小或位置不同的正方形的个数为
| A.64 | B.128 | C.204 | D.408 |
C
解析试题分析:分别找到边长为1到8的正方形的个数相加即可。解:共有1个8×8的正方形;4个7×7的正方形;9个6×6的正方形; 16个5×5的正方形;25个4×4的正方形;36个3×3的正方形; 49个2×2的正方形;64个1×1的正方形,总计204个正方形,故答案为C.
考点:认识平面图形
点评:解决本题的关键是得到边长为1到8的各种正方形的具体数目.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
设函数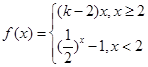 ,
,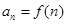 ,若数列
,若数列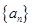 是单调递减数列,则实数
是单调递减数列,则实数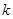 的取值范围为( )
的取值范围为( )
A.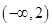 | B.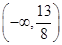 | C. | D.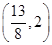 |
已知数列 满足
满足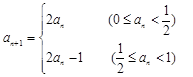 若
若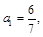 则
则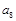 的值为( )
的值为( )
A.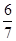 | B.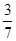 | C.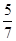 | D.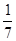 |
已知数列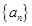 满足
满足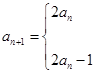
 ,若
,若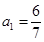 ,则
,则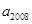 的值为( )
的值为( )
A.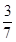 | B.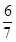 | C.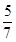 | D.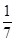 |
若数列{an}满足 ,则a2007的值 ( )
,则a2007的值 ( )
| A.1 | B.-1 | C.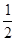 | D.2 |
在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+ a4+ a5="(" )
| A.33 | B.72 | C.84 | D.189 |
已知数列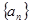 的前
的前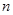 项和
项和 ,第
,第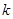 项满足
项满足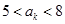 ,则
,则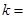
| A.9 | B.8 | C.7 | D.6 |
 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为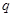 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )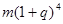 元
元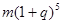 元
元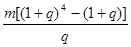 元
元 元
元