题目内容
【题目】三角形ABC中,角A、B、C所对边分别为a,b,c,且![]() .
.
(1)若cosA=![]() ,求sinC的值;
,求sinC的值;
(2)若b=![]() ,a=3c,求三角形ABC的面积.
,a=3c,求三角形ABC的面积.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据a2+c2=b2+ac.由余弦定理求出cosB,cosA![]() ,再求解sinA,sinB,根据sinC=sin(B+A)打开即可求解.(2)由a2+c2=b2+ac.b
,再求解sinA,sinB,根据sinC=sin(B+A)打开即可求解.(2)由a2+c2=b2+ac.b![]() ,a=3c,根据余弦定理求解a,c的值,即可求出三角形ABC的面积.
,a=3c,根据余弦定理求解a,c的值,即可求出三角形ABC的面积.
(1)由余弦定理,cosB![]() .又B为三角形内角,则B=
.又B为三角形内角,则B=![]() .
.
因为cosA=![]() ,且A为三角形内角,则sinA=
,且A为三角形内角,则sinA=![]() ,
,
故sinC=sin(B+A)=sin(![]() +A)=
+A)= ![]() cosA+
cosA+![]() sinA=
sinA=![]() .
.
(2)由a=3c,由余弦定理知:b2= a2+c2-2accosB,则7=9c2+c2-3c2,解得c=1,则a=3.面积S=![]() acsinB=
acsinB=![]() .
.

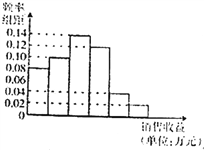
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)该公司按照类似的研究方法,测得另外一些数据,并整理得到上表:
表中的数据显示![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若广告投入![]() 万元时,实际销售收益为
万元时,实际销售收益为![]() 万元,求残差
万元,求残差![]() .
.
附: ,
,![]()
【题目】某中学将100名髙一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”

| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面2 x2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: 

