题目内容
16．用五点法画出函数y=1-sinx（x∈[0，2π]）的简图，并判断函数的单调性．分析 由题意用五点法即可画出函数图象，结合函数图象即可写出单调区间．
解答 
解：函数图象如图所示：
由图象可知该函数在$[{0，\frac{π}{2}}]$上是减少的，在$[{\frac{π}{2}，\frac{3}{2}π}]$上是增加的，在$[{\frac{3}{2}π，2π}]$上是减少的．
点评 本题主要考查了正弦函数的图象和性质，考查了五点法作图，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．下列命题中正确是（ ）
| A． | y=sinx为奇函数 | B． | y=|sinx|既不是奇函数也不是偶函数 | ||
| C． | y=3sinx+1为偶函数 | D． | y=sinx-1为奇函数 |
1．
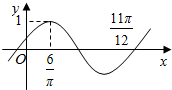函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$），f（x）的部分图象如图示，则关于y=f（x）错误的是（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$），f（x）的部分图象如图示，则关于y=f（x）错误的是（ ）| A． | 最小正周期为π | |
| B． | 向右平移$\frac{π}{6}$个单位得到函数y=sin（2x-$\frac{π}{6}$） | |
| C． | 在区间[0，$\frac{π}{2}$]上的值域为[-$\frac{1}{2}，\frac{1}{2}$] | |
| D． | 向左平移$\frac{π}{6}$个单位得到的图象关于y轴对称 |
8．双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$，则（ ）
| A． | $m＞\frac{1}{2}$ | B． | m≥1 | C． | m＞1 | D． | m＞2 |
5．数列{an}满足a1=1，且对于任意的n∈N*都满足an+1=$\frac{{a}_{n}}{3{a}_{n}+1}$，则数列{anan+1}的前n项和为 （ ）
| A． | $\frac{1}{3n+1}$ | B． | $\frac{n}{3n+1}$ | C． | $\frac{1}{3n-2}$ | D． | $\frac{n}{3n-2}$ |
6．下列命题中，正确是（ ）
| A． | 两个向量相等，则它们的起点相同，终点也相同 | |
| B． | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C． | 四边形ABCD中，一定有$\overrightarrow{AB}$=$\overrightarrow{DC}$ | |
| D． | 若$\overrightarrow{m}$=$\overrightarrow{n}$，$\overrightarrow{n}$=$\overrightarrow{p}$，则$\overrightarrow{m}$=$\overrightarrow{p}$ |