题目内容
已知α,β是三次函数f(x)=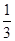 x3+
x3+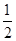 ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
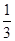 x3+
x3+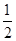 ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.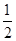
解:由函数f(x)=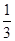 x3+
x3+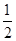 ax2+2bx(a,b∈R)可得,
ax2+2bx(a,b∈R)可得,
f′(x)=x2+ax+2b,
由题意知α,β是方程x2+ax+2b=0的两个根,
且α∈(0,1),β∈(1,2),

因此得到可行域
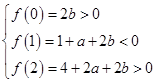
即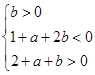 ,画出可行域如图.
,画出可行域如图.
∴动点(a,b)所在的区域面积S=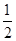 .
.
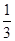 x3+
x3+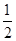 ax2+2bx(a,b∈R)可得,
ax2+2bx(a,b∈R)可得,f′(x)=x2+ax+2b,
由题意知α,β是方程x2+ax+2b=0的两个根,
且α∈(0,1),β∈(1,2),

因此得到可行域
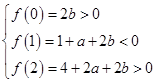
即
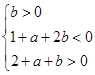 ,画出可行域如图.
,画出可行域如图.∴动点(a,b)所在的区域面积S=
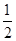 .
.
练习册系列答案
相关题目
 下,当
下,当 时,目标函数
时,目标函数 的最大值的变化范围是( )
的最大值的变化范围是( ) 



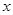 、
、 满足
满足 ,则
,则 的最小值为 .
的最小值为 . 满足约束条件
满足约束条件 ,若
,若 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数 的值为( )
的值为( )


 ,则z=(x+1)2+y2的最大值为( )
,则z=(x+1)2+y2的最大值为( )
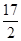
 ,动点
,动点 的坐标满足条件
的坐标满足条件 则
则 的最小值为( )
的最小值为( )


 满足约束条件
满足约束条件 那么
那么 的最大值为______.
的最大值为______.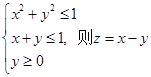 的取值范围是________.
的取值范围是________.