题目内容
【题目】如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M. 
(1)求证:O、B、D、E四点共圆;
(2)求证:2DE2=DMAC+DMAB.
【答案】
(1)解:连接BE、OE,则
∵AB为圆0的直径,∴∠AEB=90°,得BE⊥EC,
又∵D是BC的中点,
∴ED是Rt△BEC的中线,可得DE=BD.
又∵OE=OB,OD=OD,∴△ODE≌△ODB.
可得∠OED=∠OBD=90°,
因此,O、B、D、E四点共圆
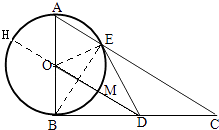
(2)解:延长DO交圆O于点H,
∵DE⊥OE,OE是半径,∴DE为圆O的切线.
可得DE2=DMDH=DM(DO+OH)=DMDO+DMOH.
∵OH= ![]() ,OD为△ABC的中位线,得DO=
,OD为△ABC的中位线,得DO= ![]() ,
,
∴ ![]() ,化简得2DE2=DMAC+DMAB
,化简得2DE2=DMAC+DMAB
【解析】(1)连接BE、OE,由直径所对的圆周角为直角,得到BE⊥EC,从而得出DE=BD= ![]() ,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DMDH,再将DH分解为DO+OH,并利用
,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DMDH,再将DH分解为DO+OH,并利用
OH= ![]() 和DO=
和DO= ![]() ,化简即可得到等式2DE2=DMAC+DMAB成立.
,化简即可得到等式2DE2=DMAC+DMAB成立.

练习册系列答案
相关题目