Question

【题目】某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖)．

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域；

(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价．

Answer 1

【答案】(1) ，定义域为[12.5,16]；(2)当污水处理池的长为16米，宽为12.5米时，总造价最低，最低价为45000元

【解析】

(1)因污水处理水池的长为x米，则宽为米，

总造价，

由题设条件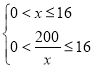

解得12.5≤x≤16，即函数定义域为[12.5,16]．

(2) ．在[0,18]上单调递减，

∴当x＝16时，y取得最小值，此时，．

综上，当污水处理池的长为16米，宽为12.5米时，总造价最低，最低价为45000元．