题目内容
(本小题满分12分)
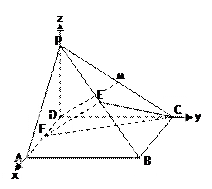
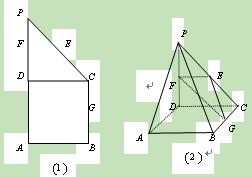
如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD 平面ABCD,PD=AB=1,E,F分别是PB,AD的中点
平面ABCD,PD=AB=1,E,F分别是PB,AD的中点
(I)证明:EF//平面PCD
(II)求二面角B-CE-F的大小

如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD
 平面ABCD,PD=AB=1,E,F分别是PB,AD的中点
平面ABCD,PD=AB=1,E,F分别是PB,AD的中点(I)证明:EF//平面PCD
(II)求二面角B-CE-F的大小

(Ⅰ)建系
如图,取PC中点M,易知: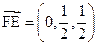 =
=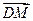 ,∴
,∴ FE∥DM
FE∥DM
又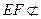
 平面PCD,
平面PCD,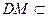 平面PCD,∴EF∥平面PCD.
平面PCD,∴EF∥平面PCD.
(Ⅱ)∵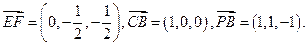
∴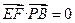 ,
,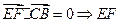 ⊥PB,EF⊥CB,又PB∩CB=B,
⊥PB,EF⊥CB,又PB∩CB=B,
 EF⊥平面PBC,而EF
EF⊥平面PBC,而EF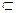 平面EFC,∴平面EFC⊥平面PBC.
平面EFC,∴平面EFC⊥平面PBC.
∴二面角B-CE-F为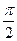 .
.

如图,取PC中点M,易知:
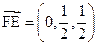 =
=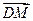 ,∴
,∴ FE∥DM
FE∥DM又
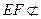
 平面PCD,
平面PCD,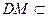 平面PCD,∴EF∥平面PCD.
平面PCD,∴EF∥平面PCD.(Ⅱ)∵
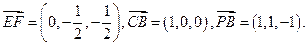
∴
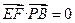 ,
,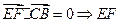 ⊥PB,EF⊥CB,又PB∩CB=B,
⊥PB,EF⊥CB,又PB∩CB=B, EF⊥平面PBC,而EF
EF⊥平面PBC,而EF 平面EFC,∴平面EFC⊥平面PBC.
平面EFC,∴平面EFC⊥平面PBC.∴二面角B-CE-F为
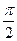 .
.略

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目

 中,
中,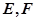 分别是
分别是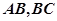 的中点,
的中点,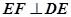 ,且
,且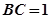 ,则正三棱锥
,则正三棱锥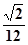
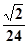
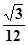
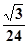
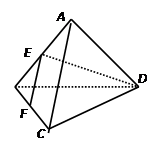
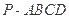 中,
中,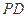 ⊥底面
⊥底面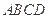
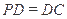 ,
,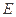 ,
,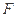 分别是
分别是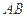
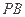 的中点.
的中点. ;(2)设PD="AD=a," 求三棱锥B-EFC的体积.
;(2)设PD="AD=a," 求三棱锥B-EFC的体积.
 柱
柱 中,
中, 侧棱与底面垂直,
侧棱与底面垂直, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.
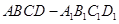 中,
中,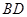 和平面
和平面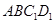 所成角的大小是( )
所成角的大小是( )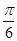
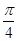
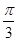
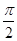

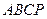 中,
中,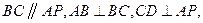
 、
、 、
、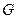 分别是线段
分别是线段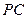 、
、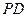 、
、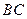 的中点,现将
的中点,现将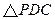 折起,使平面
折起,使平面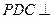 平面
平面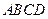 (如图(2)).
(如图(2)).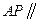 平面
平面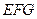 ;
;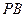 中点为
中点为 ,求证:
,求证: 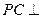 平面
平面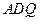 ,
,
 ,如果这三条直线将平面划
,如果这三条直线将平面划 的所有取值为 。(将你认为所有正确的序号都填上)
的所有取值为 。(将你认为所有正确的序号都填上)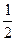 ③1 ④2 ⑤3
③1 ④2 ⑤3