题目内容
关于x的不等式x2+mx+6>0(m为常数).
(1)如果m=-5,求不等式的解集;
(2)如果不等式的解集为{x|x<1或x>6},求实数m的值.
解:(1)由m=-5,得x2-5x+6>0,即(x-2)(x-3)>0.
解得x<2或x>3.(3分)
所以原不等式的解集为{x|x<2或x>3}.(4分)
(2)根据题意,得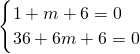 (6分)
(6分)
解得m=-7.(8分)
分析:(1)将m的值代入,将不等式的左边因式分解,得到一元二次不等式的解集.
(2)据营业处不等式的解集的形式,判断出解集的两个端点1,6是相应的方程的两个根,将根代入方程,列出方程组,求出m的值.
点评:一元二次不等式的解集的端点值是相应的一元二次方程的根.
解得x<2或x>3.(3分)
所以原不等式的解集为{x|x<2或x>3}.(4分)
(2)根据题意,得
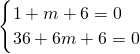 (6分)
(6分)解得m=-7.(8分)
分析:(1)将m的值代入,将不等式的左边因式分解,得到一元二次不等式的解集.
(2)据营业处不等式的解集的形式,判断出解集的两个端点1,6是相应的方程的两个根,将根代入方程,列出方程组,求出m的值.
点评:一元二次不等式的解集的端点值是相应的一元二次方程的根.

练习册系列答案
相关题目