题目内容
关于x的不等式x2-(a+1)x+a<0的解集中恰有3个整数解,则a的取值范围是
[-3,-2)∪(4,5]
[-3,-2)∪(4,5]
.分析:利用一元二次不等式的解法,解不等式,根据不等式的解集中恰有3个整数解,确定解集的取值范围,即可求解.
解答:解:由x2-(a+1)x+a<0,
得(x-1)(x-a)<0,
若a=1,则不等式无解.
若a>1,则不等式的解为1<x<a,此时要使不等式的解集中恰有3个整数解,则此时3个整数解为x=2,3,4,则4<a≤5.
若a<1,则不等式的解为a<x<1,此时要使不等式的解集中恰有3个整数解,则此时3个整数解为x=0,=-1,-2,则-3≤a<-2.
综上,满足条件的a的取值范围是[-3,-2)∪(4,5].
故答案为:[-3,-2)∪(4,5].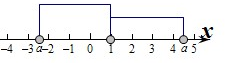
得(x-1)(x-a)<0,
若a=1,则不等式无解.
若a>1,则不等式的解为1<x<a,此时要使不等式的解集中恰有3个整数解,则此时3个整数解为x=2,3,4,则4<a≤5.
若a<1,则不等式的解为a<x<1,此时要使不等式的解集中恰有3个整数解,则此时3个整数解为x=0,=-1,-2,则-3≤a<-2.
综上,满足条件的a的取值范围是[-3,-2)∪(4,5].
故答案为:[-3,-2)∪(4,5].

点评:本题主要考查一元二次不等式的解法以及应用,考查学生分析问题,解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目