题目内容
11.设F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,P是双曲线上的点,若它的渐近线上存在一点Q(第一象限内),使得$\overrightarrow{FP}$=3$\overrightarrow{PQ}$,则双曲线离心率的取值范围为(1,4].分析 设出双曲线的右焦点,一条渐近线,以及右顶点,求出FP的最小值,即有3a不大于c-a,再由离心率公式计算即可得到.
解答 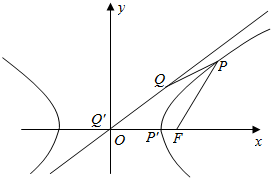 解:设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点F(c,0),
解:设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点F(c,0),
一条渐近线方程为y=$\frac{b}{a}$x,
右顶点为P′(a,0),
由|FP|≥|FP′|=c-a,
当P与P′重合,Q与O重合,则有|OP′|=a,
则3a≥c-a,即为c≤4a,
即有e=$\frac{c}{a}$≤4,
由于e>1,则1<e≤4.
故答案为:(1,4].
点评 本题考查双曲线的方程和性质,考查双曲线的点到焦点的距离的最小值,考查离心率的求法,属于基础题.

练习册系列答案
相关题目
1.已知函数f(x)=logsinβ(x2+ax+3)在区间(-∞,1)上递增,则实数a的取值范围是( )
| A. | (-4,-2] | B. | [-4,-2] | C. | (-4,+∞) | D. | (-∞,-2) |
2.已知函数$f(x)=\sqrt{3}sinωx+cosωx(ω>0)$的最小正周期为π.对于函数f(x),下列说法正确的是( )
| A. | 在$[\frac{π}{6},\frac{2π}{3}]$上是增函数 | |
| B. | 图象关于直线$x=\frac{5π}{12}$对称 | |
| C. | 图象关于点$(-\frac{π}{3},0)$对称 | |
| D. | 把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位,所得函数图象关于y轴对称 |
19.设集合A={1,3},集合B={1,2,5},则集合A∪B=( )
| A. | {1,2,5} | B. | {1} | C. | {1,2,3,5} | D. | {2,3,5} |
20.若sinα>0,则( )
| A. | cos2α>0 | B. | tan2α>0 | C. | $cos\frac{α}{2}>0$ | D. | $tan\frac{α}{2}>0$ |