题目内容
10.设函数f(x)=x2-2|x|-3,(x∈[-4,4]).(1)求证:f(x)是偶函数;
(2)画出函数f(x)的图象,并指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是单调递增还是单调递减;
(3)求函数f(x)的值域.
分析 (1)通过函数的定义域以及判断f(-x)=f(x),证明f(x)是偶函数.
(2)去掉绝对值符号,得到函数的解析式,然后画出函数的图象.写出函数f(x)的单调区间.
(3)分别通过当x≥0时,当x<0时,求出函数f(x的最小值,最大值,得到函数f(x)的值域.
解答 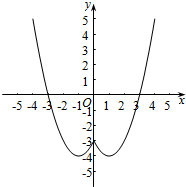 解:(1)因为x∈[-4,4],所以f(x)的定义域关于原点对称.
解:(1)因为x∈[-4,4],所以f(x)的定义域关于原点对称.
对定义域内的每一个x,都有f(-x)=f(x),所以f(x)是偶函数.
(2)当0≤x≤4时,f(x)=x2-2x-3=(x-1)2-4;
当-4≤x<0时,f(x)=x2+2x-3=(x+1)2-4.
函数f(x)的图象如图所示.
由图知函数f(x)的单调区间为
[-4,-1),[-1,0),[0,1),[1,4].
f(x)在区间[-4,-1)和[0,1)上单调递减,
在[-1,0)和[1,4]上单调递增.
(3)当x≥0时,函数f(x)=(x-1)2-4的最小值为-4,最大值为f(4)=5;
当x<0时,函数f(x)=(x+1)2-4的最小值为-4,最大值为f(-4)=5.
故函数f(x)的值域为[-4,5].
点评 本题考查函数的图象的作法,二次函数的性质的应用,函数的最值以及单调区间的求法,考查计算能力.

练习册系列答案
相关题目
1.如果函数f(x)=ax+b的图象经过第一、二、四象限,不经过第三象限,那么一定有( )
| A. | 0<a<1,-1<b<0 | B. | 0<a<1,b<-1 | C. | a>1,b<-1 | D. | a>1,-1<b<0 |
18.若实数x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥2}\\{x≤1}\end{array}\right.$,则2x+y的最大值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | $\frac{5}{2}$ |
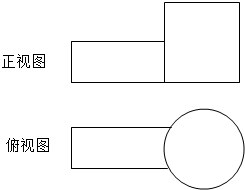 如图是某几何体的正视图和俯视图,试分析此几何体的结构特征,并画出其侧视图.
如图是某几何体的正视图和俯视图,试分析此几何体的结构特征,并画出其侧视图.