题目内容
导函数 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )
 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )A. | B.16 | C.0 | D.5 |
C
试题分析:令
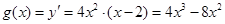 ,所以
,所以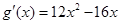 ,令
,令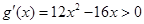 得
得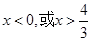 ,因为
,因为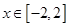 ,所以
,所以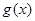 在
在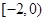 上单调递增,在
上单调递增,在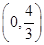 上单调递减,在
上单调递减,在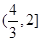 上单调递增,又因为
上单调递增,又因为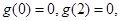 所以导函数
所以导函数 在[-2,2]上的最大值为0.
在[-2,2]上的最大值为0.点评:若求函数在闭区间上的最值,需要先求出极值,再比较极值与区间端点值的大小.

练习册系列答案
相关题目
题目内容
 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )A. | B.16 | C.0 | D.5 |
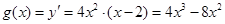 ,所以
,所以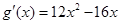 ,令
,令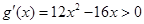 得
得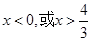 ,因为
,因为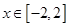 ,所以
,所以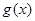 在
在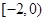 上单调递增,在
上单调递增,在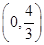 上单调递减,在
上单调递减,在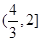 上单调递增,又因为
上单调递增,又因为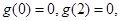 所以导函数
所以导函数 在[-2,2]上的最大值为0.
在[-2,2]上的最大值为0.