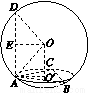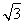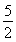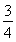题目内容
已知正三棱锥P－ABC，点P，A，B，C都在半径为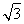
的球面上．若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为________．
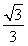
【解析】本题主要考查球的概念与性质．解题的突破口为解决好点P到截面ABC的距离．
由已知条件可知，以PA，PB，PC为棱的正三棱锥可以补充成球的内接正方体，故而PA2＋PB2＋PC2＝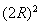
， 由已知PA＝PB＝PC, 得到PA＝PB＝PC＝2, 因为VP－ABC＝VA－PBC⇒
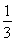h·S△ABC＝
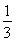PA·S△PBC, 得到h＝
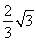，故而球心到截面ABC的距离为R－h＝.
练习册系列答案
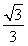名师伴你成长课时同步学练测系列答案
相关题目
设y＝f(t)是某港口水的深度y(单位：m)关于时间t的函数，其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
经长期观察，函数y＝f(t)的图像可以近似地看成函数y＝h＋Asin(ωx＋φ)的图像．最能近似表示表中数据间对应关系的函数是____________________．