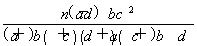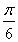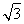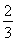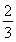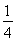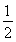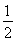题目内容
已知函数f(x)=ln(x+1)-x2-x.
(1)若关于x的方程f(x)=-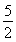 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(2)证明:对任意的正整数n,不等式2+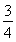 +
+ +…+
+…+ >ln(n+1)都成立.
>ln(n+1)都成立.
(1) ln 3-1≤b<ln 2+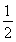 . (2)见解析
. (2)见解析
【解析】(1)f(x)=ln(x+1)-x2-x,由f(x)=-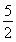 x+b,得ln(x+1)-x2+
x+b,得ln(x+1)-x2+ x-b=0,
x-b=0,
令φ(x)=ln(x+1)-x2+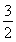 x-b,则f(x)=-
x-b,则f(x)=-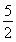 x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)=
x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)=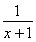 -2x+
-2x+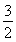 =
= 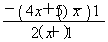 ,
,
当x∈[0,1)时,φ′(x)>0,于是φ(x)在[0,1)上单调递增;
当x∈(1,2]时,φ′(x)<0,于是φ(x)在(1,2]上单调递减.
依题意有
解得ln 3-1≤b<ln 2+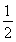 .
.
(2)证明:方法一,f(x)=ln(x+1)-x2-x的定义域为{x|x>-1},则有f′(x)=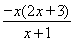 ,
,
令f′(x)=0,得x=0或x=-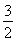 (舍去),
(舍去),
当-1<x<0时,f′(x)>0,f(x)单调递增;
当x>0时,f′(x)<0,f(x)单调递减.
∴f(0)为f(x)在(-1,+∞)上的最大值.
∴f(x)≤f(0),故ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立).
对任意正整数n,取x= >0得,ln
>0得,ln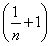 <
<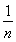 +
+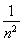 ,
,
∴ln <
<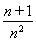 .
.
故2+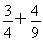 +…+
+…+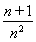 ≥ln 2+ln
≥ln 2+ln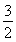 +…+ln
+…+ln 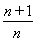 =ln(n+1).
=ln(n+1).
方法二,数学归纳法证明:
当n=1时,左边=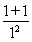 =2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.
=2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.
假设当n=k(k∈N*,k≥1)时,2+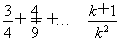 >ln(k+1)成立,
>ln(k+1)成立,
则当n=k+1时,有2+ +ln(k+1).
+ln(k+1).
做差比较:ln(k+2)-ln(k+1)-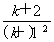 =ln
=ln 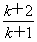 -
-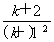 =ln
=ln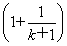 -
-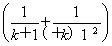 .
.
构建函数F(x)=ln(1+x)-x-x2,x∈(0,1),
则F′(x)= <0,
<0,
∴F(x)在(0,1)上单调递减,∴F(x)<F(0)=0.
取x= (k≥1,k∈N*),ln
(k≥1,k∈N*),ln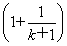 -
-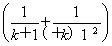 <F(0)=0.
<F(0)=0.
即ln(k+2)-ln(k+1)-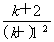 <0,
<0,
亦即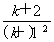 +ln(k+1)>ln(k+2),
+ln(k+1)>ln(k+2),
故n=k+1时,有2+ +ln(k+1)>ln(k+2),不等式也成立.
+ln(k+1)>ln(k+2),不等式也成立.
综上可知,对任意的正整数,不等式都成立.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表:
| 几何证明选讲 | 坐标系与 参数方程 | 不等式选讲 | 合计 |
男同学(人数) | 12 | 4 | 6 | 22 |
女同学(人数) | 0 | 8 | 12 | 20 |
合计 | 12 | 12 | 18 | 42 |
(1)在统计结果中,如果把几何证明选讲和坐标系与参数方程称为几何类,把不等式选讲称为代数类,我们可以得到如下2×2列联表:
| 几何类 | 代数类 | 总计 |
男同学(人数) | 16 | 6 | 22 |
女同学(人数) | 8 | 12 | 20 |
总计 | 24 | 18 | 42 |
据此统计你是否认为选做“几何类”或“代数类”与性别有关?若有关,你有多大的把握?
(2)在原统计结果中,如果不考虑性别因素,按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈.已知这名班级学委和两名数学科代表都在选做“不等式选讲”的同学中.
①求在这名班级学委被选中的条件下,两名数学科代表也被选中的概率;
②记抽到数学科代表的人数为X,求X的分布列及数学期望E(X).
下面临界值表仅供参考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:K2=