题目内容
f(x)= 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).
 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).| A.当k=0时,有无数个零点, |
| B.当k<0时,有3个零点 |
| C.当k>0时,有3个零点 |
| D.无论k取何值,都有4个零点 |
A
当k=0时,f(x)= 当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
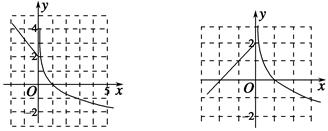
当k>0时,由图可知:f(x)=2有两根,所以由f[f(x)]=2得:f(x)=0或f(x)=e-2,又f(x)=0有两根,f(x)=e-2有两根,所以f[f(x)]=2有四根.
 当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
当k>0时,由图可知:f(x)=2有两根,所以由f[f(x)]=2得:f(x)=0或f(x)=e-2,又f(x)=0有两根,f(x)=e-2有两根,所以f[f(x)]=2有四根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, .
.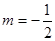 ,求证:函数
,求证:函数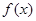 是
是 上的奇函数;
上的奇函数;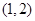 上没有零点,求实数
上没有零点,求实数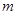 的取值范围.
的取值范围.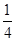 ,
,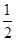
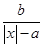 (a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.
(a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.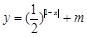 的图像与
的图像与 轴有公共点,则
轴有公共点,则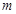 的取值范围是( )
的取值范围是( )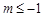
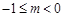
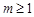
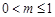
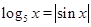 的解的个数为( )
的解的个数为( )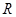 的偶函数
的偶函数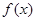 ,对于任意
,对于任意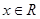 ,满足
,满足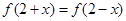 ,且当
,且当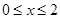 时
时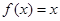 .令
.令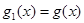 ,
,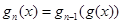 ,其中
,其中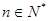 ,函数
,函数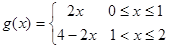 。则方程
。则方程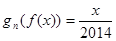 的解的个数为______________(结果用
的解的个数为______________(结果用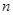 表示).
表示).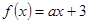 在
在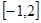 上存在零点”的充要条件是 .
上存在零点”的充要条件是 .