题目内容
【题目】在直角坐标系xOy中,已知椭圆E的中心在原点,长轴长为8,椭圆在X轴上的两个焦点与短轴的一个顶点构成等边三角形.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 过椭圆内一点
过椭圆内一点![]() 的直线与椭圆E交于不同的A,B两点,交直线
的直线与椭圆E交于不同的A,B两点,交直线![]() 于点N,若
于点N,若![]() ,求证:
,求证:![]() 为定值,并求出此定值.
为定值,并求出此定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由长轴为8,得![]() ,由两个焦点与短轴的一个顶点构成等边三角形,可得
,由两个焦点与短轴的一个顶点构成等边三角形,可得![]() ,从而可得结果;(2)设
,从而可得结果;(2)设![]() ,由
,由![]() 可得
可得![]() ,代入椭圆方程得到
,代入椭圆方程得到![]() ,同理可得
,同理可得![]() ,利用韦达定理可得结果.
,利用韦达定理可得结果.
(1)因为长轴为8,所以![]() ,
,
又因为两个焦点与短轴的一个顶点构成等边三角形,
所以![]() ,由于椭圆焦点在
,由于椭圆焦点在![]() 轴上,
轴上,
所以椭圆的标准方程为:![]() ;
;
(2)设![]() ,由
,由![]()
得![]() ,
,
所以![]() ,
,
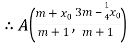 ,因为
,因为![]() 上,所以得到
上,所以得到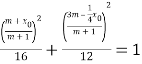 ,
,
得到![]() ;
;
同理,由![]() 可得
可得![]() ,
,
所以m,n可看作是关于x的方程![]() 的两个根,
的两个根,
所以![]() ,为定值.
,为定值.

【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: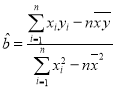 ,
,![]() ,
,![]() ,
,![]() .
.
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: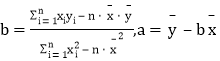 ,
,![]() ,
,![]()

![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?