Question

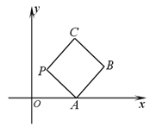
【题目】如图所示，在平面直角坐标系上放置一个边长为1的正方形，此正方形沿轴滚动（向左或向右均可），滚动开始时，点位于原点处，设顶点的纵坐标与横坐标的函数关系式，，该函数相邻两个零点之间的距离为.

（1）写出的值并求出顶点到的最小运动路径的长度的值；

（2）写出函数，，的表达式；并研究该函数除周期外的基本性质（无需证明）.

Answer 1

【答案】（1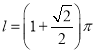），；（2）函数，，

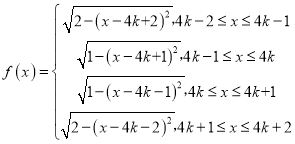奇偶性：偶函数；递增区间：，；递减区间，；零点：，.

【解析】

（1）画出点的运动轨迹，即可得出与的值.

（2）根据所画的点的运动轨迹，即可写出函数，，的表达式与函数的基本性质.

（1）点的运动轨迹如图所示：

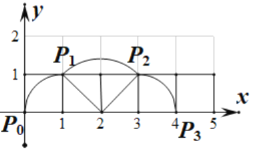
因为正方形的周长为4,所以.

当，点运动路径的长度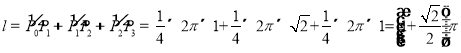

（2） 当，时，其为以为圆心，为半径的圆在的部分，即.

当，时，其为以为圆心，为半径的圆在的部分，即

当，时，其为以为圆心，为半径的圆在的部分，即.

当，时，其为以为圆心，为半径的圆在的部分，即.

所以函数，，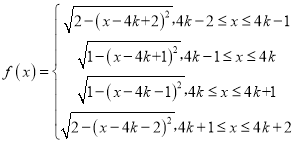

由图可知：

奇偶性：偶函数；递增区间：，；递减区间，；零点：，.