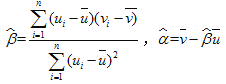题目内容
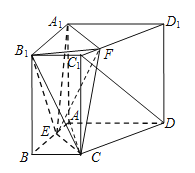
【题目】如图,在三棱锥P-ABC中,![]() ,平面
,平面![]() 平面ABC,点D在线段BC上,且
平面ABC,点D在线段BC上,且![]() ,E,F分别为线段PC,AB的中点,点G是PD上的动点.
,E,F分别为线段PC,AB的中点,点G是PD上的动点.
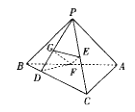
(1)证明:![]() .
.
(2)当![]() 平面PAC时,求直线PA与平面EFG所成角的正弦值.
平面PAC时,求直线PA与平面EFG所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1) 连接PF,先证明![]() 平面PDF,再证明
平面PDF,再证明![]() 即可.
即可.
(2) F为坐标原点,以FH.FA,FP所在直线为坐标轴建立空间直角坐标系F-xyz,再根据空间向量中直线与平面夹角的方法求解即可.
(1)证明:连接PF,因为![]() ,F为AB的中点,
,F为AB的中点,
所以![]() .
.
又平面![]() 平面ABC,平面
平面ABC,平面![]() 平面
平面![]() ,
,
所以![]() 平面ABC,从而
平面ABC,从而![]() .
.
设BC的中点H,因为![]() ,DF是
,DF是![]() 的中位线,
的中位线,
所以![]() .
.
同理可知![]() ,所以
,所以![]()
所以![]() 平面PDF
平面PDF
因为![]() 平面PDF,所以
平面PDF,所以![]()
(2)解:连接GH,因为FH是![]() 的中位线,所以
的中位线,所以![]() .
.
因为![]() 平面PAC,
平面PAC,![]() 平面PAC,所以
平面PAC,所以![]() 平面PAC.
平面PAC.
又因为![]() 平面PAC,
平面PAC, ![]() ,所以平面
,所以平面![]() 平面PAC
平面PAC
因为平面PBC分别与平面FGH与PAC相交于GH,PC,
所以![]() ,且
,且![]()
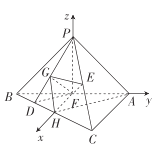
易知FH,FA,FP两两垂直,以F为坐标原点,以FH.FA,FP所在直线为坐标轴建立空间直角坐标系F-xyz,如图所示,

则![]() .
.
![]()
设平面EFG的法向量为![]() ,
,
由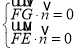 得
得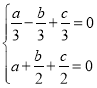 ,取
,取![]() ,得
,得![]()
又![]() ,设PA与平面EFG所成角为
,设PA与平面EFG所成角为![]()
则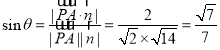

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
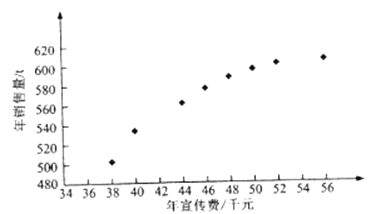
(![]() =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: