题目内容
【题目】在下列命题中,正确的命题有________(填写正确的序号)
①若![]() ,则
,则![]() 的最小值是6;
的最小值是6;
②如果不等式![]() 的解集是
的解集是![]() ,那么
,那么![]() 恒成立;
恒成立;
③设x,![]() ,且
,且![]() ,则
,则![]() 的最小值是
的最小值是![]() ;
;
④对于任意![]() ,
,![]() 恒成立,则t的取值范围是
恒成立,则t的取值范围是![]() ;
;
⑤“![]() ”是“复数
”是“复数![]() (
(![]() )是纯虚数”的必要非充分条件;
)是纯虚数”的必要非充分条件;
⑥若![]() ,
,![]() ,
,![]() ,则必有
,则必有![]() ;
;
【答案】①②③④⑥
【解析】
①![]() ,利用均值定理求最值即可;
,利用均值定理求最值即可;
②由一元二次不等式与一元二次方程的关系,利用韦达定理求解即可;
③由![]() 得
得![]() ,代入式子中可得关于
,代入式子中可得关于![]() 的函数,进而求得最值即可;
的函数,进而求得最值即可;
④设![]() ,则可转化为在
,则可转化为在![]() 时,
时,![]() ,进而求解即可;
,进而求解即可;
⑤由纯虚数的定义可知虚部不为0,实部为0,进而判断即可;
⑥由![]() 可得
可得![]() ,代入
,代入![]() 中可得
中可得![]() ,再将
,再将![]() 代入
代入![]() 求解即可
求解即可
①因为![]() ,所以
,所以![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立,故①正确;
时,等号成立,故①正确;
②由不等式与方程的关系可知![]() 和
和![]() 是方程
是方程![]() 的解,所以
的解,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,故②正确;
,故②正确;
③因为![]() ,所以
,所以![]() ,
,
则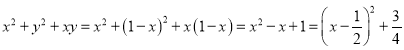 ,
,
则当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,故③正确;
,故③正确;
④由题,因为![]() ,即
,即![]() 在
在![]() 时恒成立,
时恒成立,
当![]() 时,
时,![]() ,不成立;
,不成立;
当![]() 时,设
时,设![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,
综上,![]() ,故④正确;
,故④正确;
⑤因为![]() (
(![]() )是纯虚数,所以
)是纯虚数,所以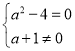 ,解得
,解得![]() 或
或![]() ,
,
所以“![]() ”是“复数
”是“复数![]() (
(![]() )是纯虚数”的充分不必要条件,故⑤错误;
)是纯虚数”的充分不必要条件,故⑤错误;
⑥因为![]() ,
,![]() ,所以
,所以![]() ,代入
,代入![]() 可得
可得![]() ,
,
则![]() ,即
,即![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以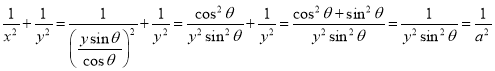 ,
,
故⑥正确;
故答案为: ①②③④⑥

练习册系列答案
相关题目