题目内容
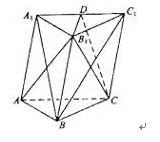
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.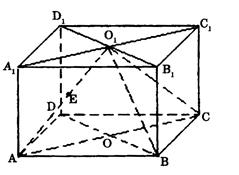
(1)求证:平面O1AC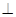 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.
(1)只需证BD⊥面O1AC即可;(2) 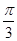 ;(3)
;(3)  。
。
解析试题分析:(1)证明:∵ABCD-A1B1C1D1是直四棱柱,∴AA1⊥面AC,又BD?面AC,所以AA1⊥BD. 又∵ABCD是菱形,∴AC⊥BD,∵AA1∩AC=A
所以BD⊥面AA1C。
即BD⊥面O1AC,又BD?面O1BD,
所以平面O1AC⊥平面O1BD.
(2)解:过O作OH⊥BC于H,连接O1H,则∠O1HO为二面角O1-BC-D的平面角.
在Rt△BHO中,OB=2,∠OBH=60°,∴OH= 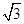
又O1O∥A1A,∴O1O⊥OH.∴tan∠O1OH= 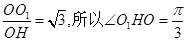 .故二面角O1-BC-D的大小为
.故二面角O1-BC-D的大小为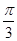 .
.
(3)因为E为AO1的中点,所以OE//O1C,所以E到面O1BC的距离等于O到面O1BC的距离,根据等积法 即可求出点E到平面O1BC的距离为
即可求出点E到平面O1BC的距离为 。
。
考点:面面垂直的判定定理;二面角;点到面的距离。
点评:本题以直四棱柱为载体,考查面面垂直,考查面面角,解题的关键是利用面面垂直的判定,正确作出面面角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.

 中,
中,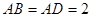 ,
,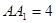 ,点
,点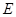 在
在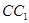 上,且
上,且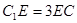 .
.
 平面
平面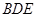 ;
;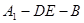 的余弦值.
的余弦值.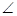 BCD=60
BCD=60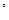 ,E是CD的中点,PA
,E是CD的中点,PA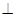 底面ABCD,PA=2.
底面ABCD,PA=2.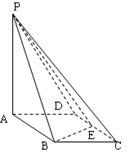
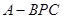 中,
中, ,
,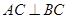 ,
, 为
为 中点,
中点,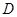 为
为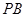 中点,且
中点,且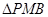 为正三角形.
为正三角形.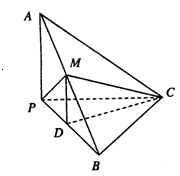
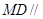 平面
平面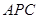 .
.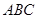 ⊥平面
⊥平面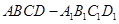 是正方体,其中
是正方体,其中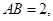
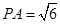
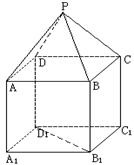
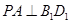 ;
;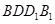 所成的锐二面角
所成的锐二面角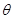 的余弦值;
的余弦值;
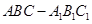 的侧面
的侧面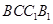 是菱形,
是菱形,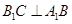
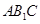
 平面
平面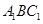 ;
; 是
是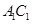 上的点,且
上的点,且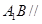 平面
平面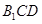 ,求
,求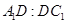 的值.
的值.