题目内容
(本小题满分12分)在直三棱柱(侧棱垂直底面) 中,
中,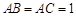 ,
,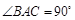 ,且异面直线
,且异面直线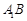 与
与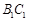 所成的角等于
所成的角等于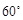 .
.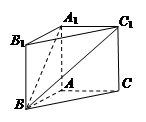
(Ⅰ)求棱柱的高;
(Ⅱ)求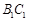 与平面
与平面 所成的角的大小.
所成的角的大小.
(1)1(2)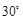
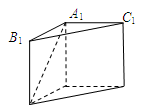
解析试题分析:解:解:(Ⅰ)由三棱柱 是直三棱柱可知,
是直三棱柱可知,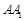 即为其高.
即为其高.
如图,因为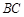 ∥
∥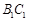 ,所以
,所以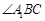 是异面直线
是异面直线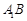 与
与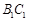 所成的角或其补角.
所成的角或其补角.
连接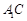 ,因为
,因为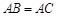 ,所以
,所以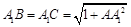 .
.
在Rt△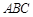 中,由
中,由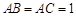 ,
,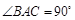 ,可得
,可得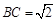 .…………… 3分
.…………… 3分
又异面直线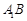 与
与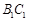 所成的角为
所成的角为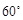 ,所以
,所以 ,即△
,即△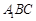 为正三角形.
为正三角形.
于是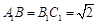 .
.
在Rt△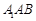 中,由
中,由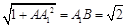 ,得
,得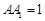 ,即棱柱的高为
,即棱柱的高为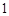 .……6分
.……6分
(Ⅱ)连结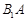 ,设
,设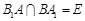 ,由(Ⅰ)知,
,由(Ⅰ)知,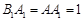 ,
,
所以矩形 是正方形,所以
是正方形,所以 .
.
又由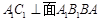 得
得 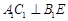 ,于是得
,于是得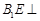 平面
平面 .
.
故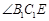 就是
就是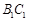 与平面
与平面 所成的角. ………………………… 9分
所成的角. ………………………… 9分
在Rt△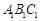 中,由
中,由 ,
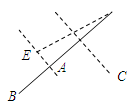
,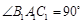 ,
,
可得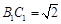 .
.
在Rt△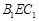 中,由
中,由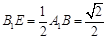 ,
,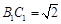 ,
,
得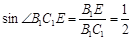 ,故
,故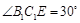 .
.
因此 与平面
与平面 所成的角
所成的角 . ………………………………………… 12分
. ………………………………………… 12分
考点:本试题考查了棱柱中距离和角的求解。
点评:对于几何体中的高的求解,可以借助于勾股定理来得到,同时对于线面角的求解,一般分为三步骤:先作,二证,三解。这也是所有求角的一般步骤,属于中档题。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
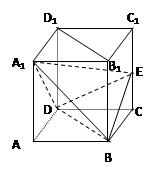
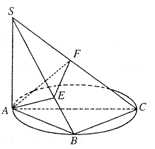
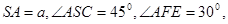 求三棱锥S—AEF的体积.
求三棱锥S—AEF的体积.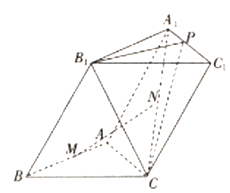
 中,
中,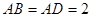 ,
,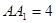 ,点
,点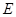 在
在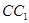 上,且
上,且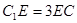 .
.
 平面
平面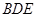 ;
;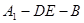 的余弦值.
的余弦值. 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
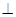 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
.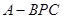 中,
中, ,
,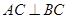 ,
, 为
为 中点,
中点,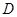 为
为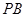 中点,且
中点,且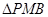 为正三角形.
为正三角形.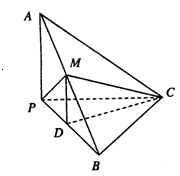
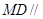 平面
平面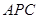 .
.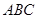 ⊥平面
⊥平面
 中,
中,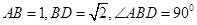 ,将它们沿对角线
,将它们沿对角线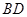 折起,折后的点
折起,折后的点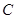 变为
变为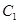 ,且
,且 .
.
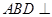 平面
平面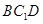 ;
;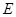 为线段
为线段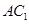 上的一个动点,当线段
上的一个动点,当线段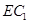 的长为多少时,
的长为多少时, 与平面
与平面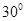 ?
?