题目内容
已知椭圆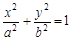
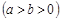 的离心率为
的离心率为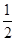 ,两焦点之间的距离为4.
,两焦点之间的距离为4.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右顶点作直线交抛物线 于A、B两点,
于A、B两点,
(1)求证:OA⊥OB;
(2)设OA、OB分别与椭圆相交于点D、E,过原点O作直线DE的垂线OM,垂足为M,证明|OM|为定值.
【答案】
(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
【解析】(1)由2c=4,c/a=1/2,可求出a,进而求出b,问题解决.
(II)(1)若直线的斜率存在,可设直线方程为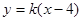
然后与抛物线方程联立,消去y转化为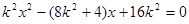 ,
,
借助韦达定理证明 即可.
即可.
斜率不存在的情况要单独考虑.
(2) 设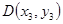 、
、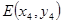 ,直线
,直线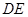 的方程为
的方程为 ,代入
,代入 ,得
,得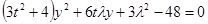 .于是
.于是 .
.
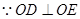 ,
,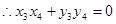 .可得
.可得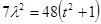 .
.
再证明原点到直线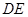 的距离
的距离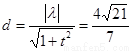 为定值
为定值
解:(Ⅰ)由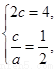 得
得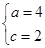 ,故
,故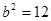 .
………………………3分
.
………………………3分
所以,所求椭圆的标准方程为 ……………………………4分
……………………………4分
(Ⅱ)(1)若直线的斜率存在,可设直线方程为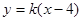 ……………5分
……………5分
代入抛物线方程整理得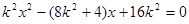
设点A(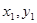 )点B(
)点B(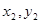 ),则
),则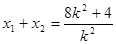 ,
,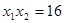 ………7分
………7分
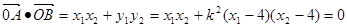
所以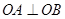 ……………………………………………9分
……………………………………………9分
若直线斜率不存在,则A(4,4)B(4,-4),同样可得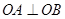 …………10分
…………10分
(2)设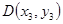 、
、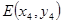 ,直线
,直线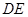 的方程为
的方程为 ,代入
,代入 ,得
,得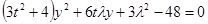 .于是
.于是 .从而
.从而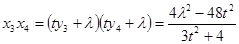
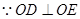 ,
,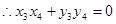 .得
.得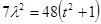 .∴原点到直线
.∴原点到直线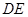 的距离
的距离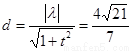 为定值…15分
为定值…15分

练习册系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: