题目内容
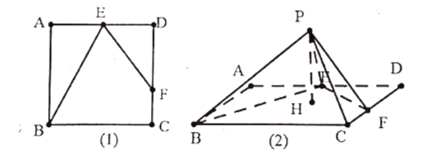
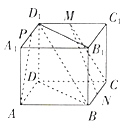
【题目】如图，在正方体ABCD﹣A1B1C1D1中，M，N，P分别是C1D1，BC，A1D1的中点，有下列四个结论：
①AP与CM是异面直线；②AP，CM，DD1相交于一点；③MN∥BD1；
④MN∥平面BB1D1D．
其中所有正确结论的编号是（ ）
A.①④B.②④C.①④D.②③④
【答案】B
【解析】
利用异面直线的概念，以及线面平行的判定定理和性质定理，逐项判定，即可求解．
因为MP∥AC，MP≠AC，所以AP与CM是相交直线，
又面A1ADD1∩面C1CDD1＝DD1，所以AP，CM，DD1相交于一点，则①不正确，②正确．
③令AC∩BD＝O，因为M，N分别是C1D1，BC的中点，
所以ON∥D1M∥CD，
，则MNOD1为平行四边形，
所以MN∥OD1，因为MN
平面BD1D，OD1平面BD1D，
所以MN∥平面BD1D，③不正确，④正确．
综上所述，可得②④正确，
故选：B．
练习册系列答案
相关题目
