题目内容
已知椭圆
+
=1 (a＞b＞0)的面积为abπ，若全集U={（x，y）|x∈R，y∈R}，
集合A={(x，y)|
+
≤1}，B={(x，y)|3x+4y+12＞0}，则A∩（?uB）所表示的图形的面积为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
集合A={(x，y)|
| x2 |
| 16 |
| y2 |
| 9 |
| A、6（π-1） |
| B、9π+6 |
| C、3π-3 |
| D、3（π-2） |
分析：根据二元一次不等式组表示平面区域，确定?uB对应的平面区域，然后确定集合A∩（?uB）对应的平面区域，然后求区域面积．
解答：解：根据集合补集的定义可知（?uB）={（x，y）|3x+4y+12≤0}，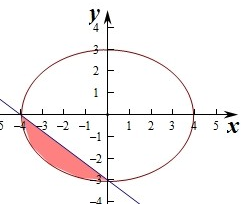
∴A∩（?uB）所表示的图形的为图中阴影部分，
∵椭圆
+
=1 (a＞b＞0)的面积为abπ，
∴对应阴影部分椭圆部分的面积为
•π×3×4=3π，
三角形的面积为
×3×4=6，
∴A∩（?uB）所表示的图形的面积为3π-6=3（π-2），
故选：D．
∴A∩（?uB）所表示的图形的为图中阴影部分，
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴对应阴影部分椭圆部分的面积为
| 1 |
| 4 |
三角形的面积为
| 1 |
| 2 |
∴A∩（?uB）所表示的图形的面积为3π-6=3（π-2），
故选：D．
点评：本题主要考查区域面积的求法，利用二元一次不等式表示平面区域是解决本题的关键，考查学生的计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目