题目内容
椭圆 的焦点
的焦点 为椭圆上的一点,已知
为椭圆上的一点,已知 ,则
,则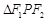 的面积为( )
的面积为( )
 的焦点
的焦点 为椭圆上的一点,已知
为椭圆上的一点,已知 ,则
,则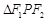 的面积为( )
的面积为( ) | A.12 | B.9 | C.8 | D.10 |
B
根据椭圆定义及条件得: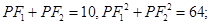 所以
所以
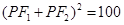 ,即
,即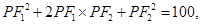
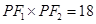 ;则
;则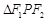 的面积为
的面积为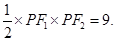 故选B
故选B
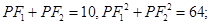 所以
所以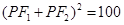 ,即
,即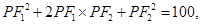
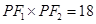 ;则
;则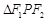 的面积为
的面积为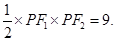 故选B
故选B
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
题目内容
 的焦点
的焦点 为椭圆上的一点,已知
为椭圆上的一点,已知 ,则
,则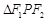 的面积为( )
的面积为( ) | A.12 | B.9 | C.8 | D.10 |
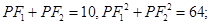 所以
所以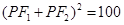 ,即
,即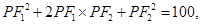
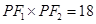 ;则
;则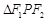 的面积为
的面积为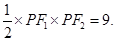 故选B
故选B
 高中必刷题系列答案
高中必刷题系列答案