Question

【题目】已知椭圆的离心率为，过的左焦点的直线，直线被圆：截得的弦长为.

（Ⅰ）求椭圆的方程；

（Ⅱ）设的右焦点为，在圆上是否存在点，满足，若存在，指出有几个这样的点（不必求出点的坐标）；若不存在，说明理由.

Answer 1

【答案】（1）（2）不存在点，满足．

【解析】试题分析：（1）直线与轴的交点为的左焦点，所以，再根据离心率得，即得，（2）先由条件确定点轨迹，为一个圆，再根据两圆位置关系确定交点个数.

试题解析：解：（Ⅰ）因为直线的方程为： ，

令，得，即．

，又，

， ，

∴椭圆的方程为．

（Ⅱ）∵圆心到直线： 的距离为，

又直线： 被圆： 截得的弦长为，

∴由垂径定理得，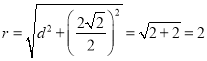

故圆的方程为： ．

设圆上存在点，满足，即，

且的坐标为，则，

整理得，它表示圆心在，半径是的圆．

，

故有，即圆与圆没有公共点．

∴圆上不存在点，满足．