题目内容
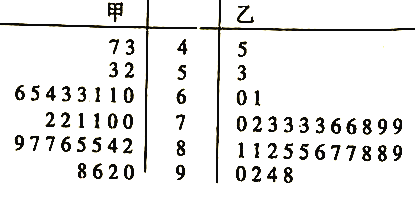
【题目】我市两所高中分别组织部分学生参加了“七五普法网络知识大赛”,现从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,得到样本数据的茎叶图如图所示.
(Ⅰ)若乙校每位学生被抽取的概率为0.15,求乙校参赛学生总人数;
(Ⅱ)根据茎叶图,从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩(不要求计算);
(Ⅲ)从样本成绩低于60分的学生中随机抽取3人,求3人不在同一学校的概率.
【答案】(1)200(2)平均水平:甲小乙大;波动情况:甲大乙小;(3)![]()
【解析】试题分析:(1)先求出甲校每位同学物理成绩被抽取的概率,由此能求出高二年级学生总数;(2)由茎叶图可知,甲校有![]() 位同学分布在
位同学分布在![]() 至
至![]() 之间,乙校有
之间,乙校有![]() 位同学分布在
位同学分布在![]() 至
至![]() 之间,能由此得到统计结论;(3)由茎叶图可知,甲校有
之间,能由此得到统计结论;(3)由茎叶图可知,甲校有![]() 位同学成绩不及格,分别记为
位同学成绩不及格,分别记为![]() ,乙校有
,乙校有![]() 位同学成绩不及格,分别记为
位同学成绩不及格,分别记为 ![]() ,由此利用列举法结合古典概型概率公式能求出至少抽到一名乙校学生的概率.
,由此利用列举法结合古典概型概率公式能求出至少抽到一名乙校学生的概率.
试题解析:(Ⅰ) ![]() (人);
(人);
(Ⅱ)平均水平:甲小乙大;波动情况:甲大乙小;
(Ⅲ)记甲校成绩低于60分的4人为1,2,3,4,乙校成绩低于60分的2人为5,6,则从中选出3人的所有基本事件为:123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456共计20个.
记“抽取的3人不在同一学校”为事件![]() ,则
,则![]() 包含的基本事件(用下划线标记)有16个,
包含的基本事件(用下划线标记)有16个,
∴![]() .
.

【题目】某市积极倡导学生参与绿色环保活动,其中代号为“环保卫士—12369”的绿色环保活动小组对2014年1月—2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: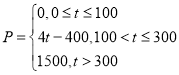 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为某市本年度空气重度污染与供暖有关?
的把握认为某市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】某市每年中考都要举行实验操作考试和体能测试,初三(1)班共有30名学生,如图表格为该班学生的这两项成绩,表中实验操作考试和体能测试都为优秀的学生人数为6人.由于部分数据丢失,只知道从这班30人中随机抽取一个,实验操作成绩合格,且体能测试成绩合格或合格以上的概率是![]() .
.
实验操作 | |||||
不合格 | 合格 | 良好 | 优秀 | ||
体能测试 | 不合格 | 0 | 1 | 1 | 1 |
合格 | 0 | 2 | 1 |
| |
良好 | 1 |
| 2 | 4 | |
优秀 | 1 | 1 | 3 | 6 | |
(Ⅰ)试确定![]() ,
, ![]() 的值;
的值;
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.