题目内容
（本小题满分14分）
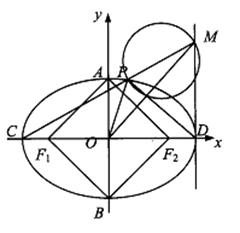
已知椭圆
的左、右焦点分别为F1、F2，短轴两个端点为A、B，且四边形F1AF2B是边长为2的正方形。
（1）求椭圆的方程；
（2）若C、D分别是椭圆长的左、右端点，动点M满足MD⊥CD，连接CM，交椭圆于点P。证明：
为定值。
（3）在（2）的条件下，试问x轴上是否存异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，求出点Q的坐标；若不存在，请说明理由。
已知椭圆
的左、右焦点分别为F1、F2，短轴两个端点为A、B，且四边形F1AF2B是边长为2的正方形。（1）求椭圆的方程；
（2）若C、D分别是椭圆长的左、右端点，动点M满足MD⊥CD，连接CM，交椭圆于点P。证明：
为定值。（3）在（2）的条件下，试问x轴上是否存异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，求出点Q的坐标；若不存在，请说明理由。
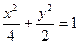，定值为4，存在Q（0，0）满足条件（1）
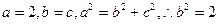
∴椭圆方程为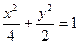 ………………4分
（2）
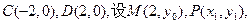
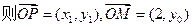
直线CM：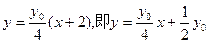
代入椭圆方程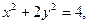
得
………………6分
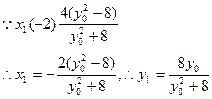
………………8分
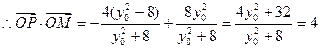（定值）…………10分
（3）设存在
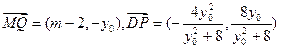
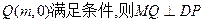……11分
则由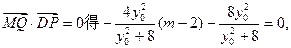
………12分
从而得m=0
∴存在Q（0，0）满足条件 ………………14分
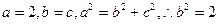
∴椭圆方程为
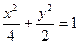………………4分（2）
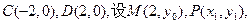
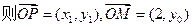
直线CM：
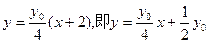
代入椭圆方程
|
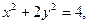
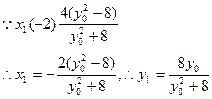
………………6分 ………………8分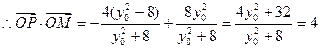（定值）…………10分（3）设存在
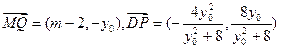
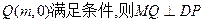……11分则由
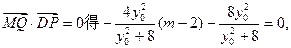………12分从而得m=0
∴存在Q（0，0）满足条件 ………………14分
练习册系列答案
相关题目
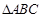中，
，
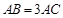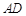是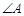
的平分线，且
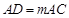，则实数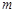
的取值范围是 ▲ ．
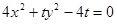的虚轴长等于( ) 
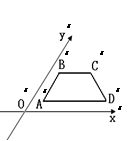
的左焦点为F，左右顶点分别为A、C，
，其中圆心P的坐标为
．
，求
上，求椭圆的方程．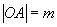
，求直线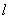
的极坐标方程。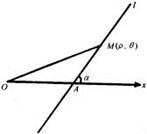
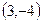与圆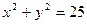
相切的直线方程是 ．
=1的左焦点F引圆x2 + y2 = 3的切线FP交双曲线右支于点P，T为切点，M为线段FP的中点，O为坐标原点，则| MO | – | MT | 等于 。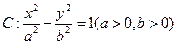
的离心率为
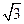，右准线为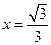
。
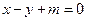与双曲线C交于不同的两点A，B，且线段AB的中点在圆
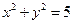上，求m的值.