题目内容
17.(1)已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a.求a的值;(2)对于实数x,y,若|x-1|≤1,|y-2|≤1,求|x-y+1|的最大值.
分析 (1)由条件利用绝对值三角不等式,求得f(x)=|x+1|+|x-2|的最小值a的值.
(2)由条件利用绝对值三角不等式,求得|x-y+1|的最大值.
解答 解:(1)定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a,f(x)=|x+1|+|x-2|≥|x+1-(x-2)|=3,
故a=3.
(2)对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-y+1|=|(x-1)-(y-2)|≤|x-1|+|y-2|≤2,
故|x-y+1|的最大值为2.
点评 本题主要考查绝对值三角不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如图,若依次输入的x分别为$\frac{5π}{6}$、$\frac{π}{6}$,相应输出的y分别为y1、y2,则y1、y2的大小关系是( )
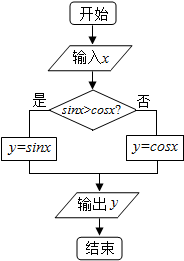

| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
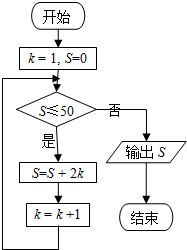
12.执行如图所示的程序框图,则输出的S值为( )


| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
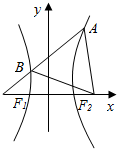 如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.
如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.