题目内容
9.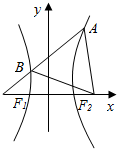 如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.
如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.
分析 由双曲线的定义,可得F1A-F2A=F1A-AB=F1B=2a,BF2-BF1=2a,BF2=4a,F1F2=2c,再在△F1BF2中应用余弦定理得,a,c的关系,由离心率公式,计算即可得到所求.
解答 解:因为△ABF2为等边三角形,不妨设AB=BF2=AF2=m,
A为双曲线上一点,F1A-F2A=F1A-AB=F1B=2a,
B为双曲线上一点,则BF2-BF1=2a,BF2=4a,F1F2=2c,
由$∠AB{F_2}={60^0}$,则$∠{F_1}B{F_2}={120^0}$,
在△F1BF2中应用余弦定理得:4c2=4a2+16a2-2•2a•4a•cos120°,
得c2=7a2,则${e^2}=7⇒e=\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查双曲线的定义、方程和性质,考查余弦定理的运用,考查运算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
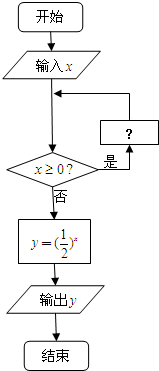
4.如图是某算法的程序框图,若输出的b值为32,则判断框内①应填( )

| A. | 4? | B. | 5? | C. | 6? | D. | 7? |
1.已知等差数列{an}前四项中第二项为606,前四项和Sn为2600,则第4项为( )
| A. | 707 | B. | 782 | C. | 870 | D. | 990 |
19.定义在R上的函数g(x)=ex+e-x+|x|,则满足g(2x-1)<g(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |