题目内容
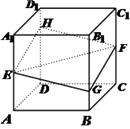
【题目】如图,正方体 ![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱 ![]() 的中点,过
的中点,过 ![]() 的平面与棱
的平面与棱 ![]() 分别交于点
分别交于点 ![]() .设
.设 ![]() ,
, ![]() .
.
①四边形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四边形
;③四边形 ![]() 的面积
的面积 ![]() 在区间
在区间 ![]() 上具有单调性;④四棱锥
上具有单调性;④四棱锥 ![]() 的体积为定值.
的体积为定值.
以上结论正确的个数是( )
A.4
B.3
C.2
D.1
【答案】B
【解析】因为对面互相平行,所以 ![]() 四边形
四边形 ![]() 一定是平行四边形;因为EF垂直平面BDD1B1,所以EF垂直GH,所以四边形
一定是平行四边形;因为EF垂直平面BDD1B1,所以EF垂直GH,所以四边形 ![]() 一定是菱形;因为AC//EF,所以
一定是菱形;因为AC//EF,所以 ![]() 平面
平面 ![]() ;四边形
;四边形 ![]() 的面积
的面积 ![]()
![]() 在区间
在区间 ![]() 上先减后增;四棱锥
上先减后增;四棱锥 ![]() 的体积为
的体积为 ![]() ,所以正确的是1,2,4.
,所以正确的是1,2,4.
所以答案是:B.
【考点精析】根据题目的已知条件,利用平面的基本性质及推论和直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取 ![]() 名同学(男
名同学(男 ![]() 人,女
人,女 ![]() 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
附表及公式: ![]()

(1)能否据此判断有 ![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的 ![]() 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为
名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ![]() ,求
,求 ![]() 的分布列和
的分布列和 ![]() .
.