题目内容
【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合是“好集合”.给出下列4个集合:①
成立,则称集合是“好集合”.给出下列4个集合:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“好集合”的序号是( )
.其中为“好集合”的序号是( )
A. ①②④ B. ②③ C. ③④ D. ①③④
【答案】B
【解析】对于①y=![]() 是以x,y轴为渐近线的双曲线,渐近线的夹角是90°,所以在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足好集合的定义;在另一支上对任意(x1,y1)∈M,不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足好集合的定义,不是好集合.
是以x,y轴为渐近线的双曲线,渐近线的夹角是90°,所以在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足好集合的定义;在另一支上对任意(x1,y1)∈M,不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足好集合的定义,不是好集合.
对于②M={(x,y)|y=ex-2},如图(2)如图红线的直角始终存在,对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,例如取M(0,-1),则N(ln2,0),满足好集合的定义,
所以是好集合;正确.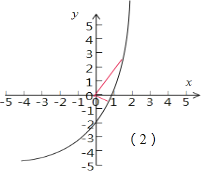
对于③M={(x,y)|y=cosx},如图(3)对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,例如(0,1)、(π,0),满足好集合的定义,所以M是好集合;正确.
对于④M={(x,y)|y=lnx},如图(4)取点(1,0),曲线上不存在另外的点,使得两点与原点的连线互相垂直,所以不是好集合.
所以②③正确.
故选B.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
