题目内容
已知数列{an}满足a1+a2+…+an=n2(n∈N*),
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对任意给定的k∈N*,是否存在p,r∈N*(k<p<r),使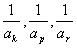 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由;
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为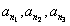 。
。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对任意给定的k∈N*,是否存在p,r∈N*(k<p<r),使
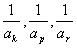 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由;
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由;(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为
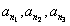 。
。 解:(Ⅰ)当n=1时,a1=1;
当n≥2,n∈N*时,a1+a2+…+an-1=(n-1)2,
所以an=n2-(n-1)2=2n-1;
综上所述,an=2n-1(n∈N*)。
(Ⅱ)当k=1时,若存在p,r使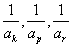 成等差数列,
成等差数列,
则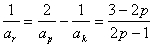 ,
,
因为p≥2,所以ar<0,与数列{an}为正数相矛盾,
因此,当k=1时不存在;
当k≥2时,设ak=x,ap=y,ar=z,则 ,
,
所以 ,
,
令y=2x-1,得z=xy=x(2x-1),
此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,
所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,
所以r=4k2-5k+2;
综上所述,当k=1时,不存在p,r;
当k≥2时,存在p=2k-1,r=4k2-5k+2满足题设;
(Ⅲ)作如下构造: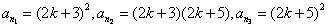 ,其中k∈N*,
,其中k∈N*,
它们依次为数列{an}中的第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13项,
显然它们成等比数列,且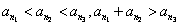 ,
,
所以它们能组成三角形,
由k∈N*的任意性,这样的三角形有无穷多个。
下面用反证法证明其中任意两个三角形A1B1C1和A2B2C2(k1≠k2)不相似;
若三角形A1B1C1和A2B2C2相似,
则 ,
,
整理得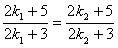 ,所以k1=k2,
,所以k1=k2,
这与条件k1≠k2相矛盾,
因此,任意两个三角形不相似;
故命题成立。
当n≥2,n∈N*时,a1+a2+…+an-1=(n-1)2,
所以an=n2-(n-1)2=2n-1;
综上所述,an=2n-1(n∈N*)。
(Ⅱ)当k=1时,若存在p,r使
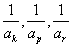 成等差数列,
成等差数列,则
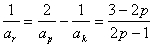 ,
,因为p≥2,所以ar<0,与数列{an}为正数相矛盾,
因此,当k=1时不存在;
当k≥2时,设ak=x,ap=y,ar=z,则
 ,
,所以
 ,
,令y=2x-1,得z=xy=x(2x-1),
此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,
所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,
所以r=4k2-5k+2;
综上所述,当k=1时,不存在p,r;
当k≥2时,存在p=2k-1,r=4k2-5k+2满足题设;
(Ⅲ)作如下构造:
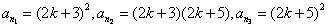 ,其中k∈N*,
,其中k∈N*,它们依次为数列{an}中的第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13项,
显然它们成等比数列,且
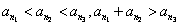 ,
,所以它们能组成三角形,
由k∈N*的任意性,这样的三角形有无穷多个。
下面用反证法证明其中任意两个三角形A1B1C1和A2B2C2(k1≠k2)不相似;
若三角形A1B1C1和A2B2C2相似,
则
 ,
,整理得
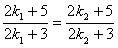 ,所以k1=k2,
,所以k1=k2,这与条件k1≠k2相矛盾,
因此,任意两个三角形不相似;
故命题成立。

练习册系列答案
相关题目