题目内容
2．求函数f（x）=$\frac{1}{8-2x-{x}^{2}}$的单调区间．分析 设t=8-2x-x2，根据复合函数单调性之间的关系进行求解即可．
解答 解：设t=8-2x-x2，有t=8-2x-x2≠0得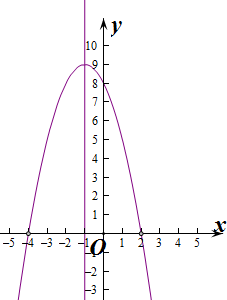
x≠2且x≠-4，
且函数的对称轴为x=-1，
由t=8-2x-x2＞0得-4＜x＜2，
由t=8-2x-x2＜0得x＜-4或x＞2，
则当x＜-4时，函数t为增函数，y=$\frac{1}{t}$为减函数，此时f（x）为减函数，
当-4＜x≤-1时，函数t为增函数，y=$\frac{1}{t}$为减函数，此时f（x）为减函数，
当-1≤x＜2时，函数t为减函数，y=$\frac{1}{t}$为减函数，此时f（x）为增函数，
当x＞2时，函数t为减函数，y=$\frac{1}{t}$为减函数，此时f（x）为增函数，
故函数的增区间为[-1，2），（2，+∞），
减区间为（-∞，-4），（-4，-1]．
点评 本题主要考查函数单调区间的求解，根据复合函数单调性之间的关系，结合一元二次函数和分式函数的单调性的性质是解决本题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
7．已知f（x）是定义在（-$\frac{π}{2}$，0）$∪（0，\frac{π}{2}）$上的奇函数，其导函数为f′（x），当x$∈（0，\frac{π}{2}）$时，f′（x）tanx-$\frac{f（x）}{co{s}^{2}x}$＞0，且f（$\frac{π}{4}$）=0，则使不等式f（x）$＜\sqrt{3}f（\frac{π}{6}）$tanx成立的x的取值范围是（ ）
| A． | （-$\frac{π}{2}，-\frac{π}{6}$）∪（$\frac{π}{6}，\frac{π}{2}$） | B． | （-$\frac{π}{6}，0$）∪（0，$\frac{π}{6}$） | C． | （-$\frac{π}{6}，0$）∪（$\frac{π}{6}，\frac{π}{2}$） | D． | （-$\frac{π}{2}，-\frac{π}{6}$）∪（0，$\frac{π}{6}$） |