题目内容
若数列
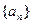 的前
的前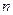 项和
项和 是
是 二项展开式中各项系数的和
二项展开式中各项系数的和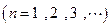 .
.(Ⅰ)求
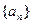 的通项公式;
的通项公式;(Ⅱ)若数列
 满足
满足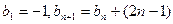 ,且
,且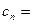
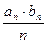 ,求数列
,求数列 的通
的通项及其前
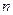 项和
项和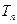 ;
;(III)求证:
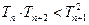 .
.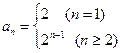 ,
,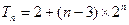
解:(Ⅰ)由题意
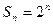 , -----------------------------------------------------2分
, -----------------------------------------------------2分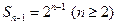 ,
,两式相减得
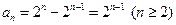 . --------------------3分
. --------------------3分当
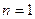 时,
时,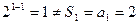 ,
,∴
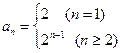 . --------------------------------------------------4分
. --------------------------------------------------4分(Ⅱ)∵
 ,
,∴
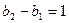 ,
,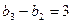 ,
,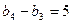 ,
,………
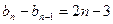 .
.以上各式相加得
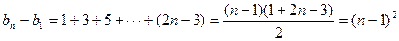 .
.∵
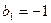 ,
,∴
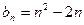 . -----------------------------------------------------------------6分
. -----------------------------------------------------------------6分∴
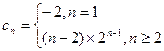 . -------------------------------------------------7分
. -------------------------------------------------7分∴
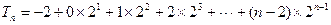 ,
,∴
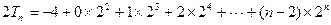 .
.∴
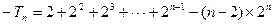 .
.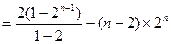
=
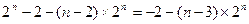 .
.∴
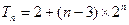 . -------------------------------------------------------------9分
. -------------------------------------------------------------9分(3)
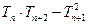 =
=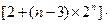
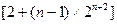
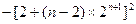
=4+
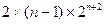
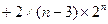
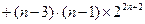
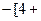
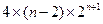
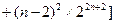
=
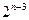
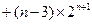
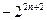
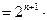
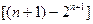 . -------------------------------------------12分
. -------------------------------------------12分∵
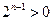 , ∴需证明
, ∴需证明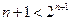 ,用数学归纳法证明如下:
,用数学归纳法证明如下:①当
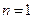 时,
时,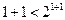 成立.
成立.②假设
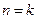 时,命题成立即
时,命题成立即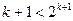 ,
,那么,当
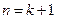 时,
时, 成立.
成立.由①、②可得,对于
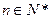 都有
都有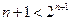 成立.
成立.∴
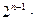
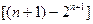
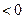 .
.∴
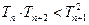 .---------------------------------------------------------------------------13分
.---------------------------------------------------------------------------13分
练习册系列答案
相关题目
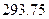 m?
m?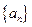 的前
的前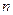 项和为
项和为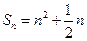 ,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么?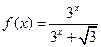 上两点
上两点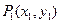 、
、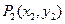 ,若
,若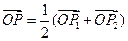 ,且
,且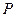 点的横坐标为
点的横坐标为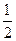
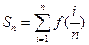 ,
,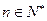 ,求
,求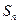 ;
;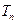 为数列
为数列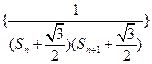 的前
的前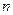 项和,若
项和,若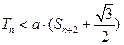 对一切
对一切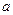 的取值范围。
的取值范围。 ,且
,且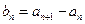 ,若
,若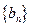 构成公差为
构成公差为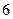 的等差数列.
的等差数列.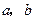 和
和 表示
表示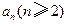 ;
;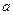 是满足
是满足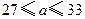 的整数,则当
的整数,则当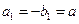 时,数列
时,数列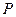 从原点出发,沿
从原点出发,沿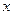 轴正向移动距离
轴正向移动距离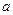 到达
到达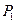 ,再沿
,再沿 轴正向移动距离
轴正向移动距离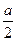 点,到达
点,到达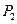 点,再沿
点,再沿 到达
到达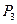 点,
点,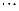 依次类推无限进行每转1次距离缩小一半.
依次类推无限进行每转1次距离缩小一半.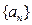 满足
满足 (
(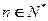 ),求证:
),求证: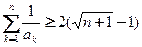 ..
..