题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有三个极值点
有三个极值点![]() ,
,![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.(2)证明见解析
单调递增.(2)证明见解析
【解析】
(1)求导,对![]() 分类讨论,确定
分类讨论,确定![]() 或
或![]() 解的区间,即可求出结论;
解的区间,即可求出结论;
(2)求![]() ,由
,由![]() ,得出
,得出![]() 或
或![]() ,
,![]() 有三个极值点,转化为
有三个极值点,转化为![]() 有两个异于2的实根.不妨设
有两个异于2的实根.不妨设![]() ,
,![]() ,根据(1)得
,根据(1)得![]() ,且
,且![]() ,从而
,从而![]() ,由零点存在定理可得
,由零点存在定理可得![]() ,又
,又![]() 时,
时,![]() ,求出实数
,求出实数![]() 的取值范围是
的取值范围是![]() .要证
.要证![]() ,只需证明
,只需证明![]() ,利用
,利用![]() ,
,![]() 是
是![]() 的两个实根,可得
的两个实根,可得![]() ,
,![]() .令
.令![]() ,则
,则![]() ,
,![]() ,
,![]() ,只需证明
,只需证明![]() ,即证
,即证![]() ,
,![]() ,令
,令![]() ,
,![]() ,利用求导,求出
,利用求导,求出![]() 单调区间,最值,即可证明结论.
单调区间,最值,即可证明结论.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)由已知得![]() ,
,![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
要使函数![]() 有三个极值点,须
有三个极值点,须![]() 有三个不相等实数根,
有三个不相等实数根,
从而![]() 有两个异于2的实根.不妨设
有两个异于2的实根.不妨设![]() ,
,![]() ,
,
由(1)知:![]() ,且
,且![]() ,从而
,从而![]() .
.
而当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
由零点存在定理知![]() .
.
又当![]() 时,
时,![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .
.
要证![]() ,只需证
,只需证![]() .①
.①
因为![]() ,
,![]() 是
是![]() 的两个实根,且
的两个实根,且![]() ,
,
所以![]() ,从而
,从而![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
要证①式成立,只需证![]() ,即证
,即证![]() ,
,![]() .
.
令![]() ,
,![]() ,则
,则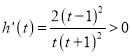 ,所以
,所以![]() 在
在![]() 递增,
递增,
所以![]() ,所以
,所以![]() .命题得证.
.命题得证.

【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
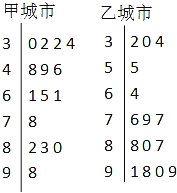
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.