题目内容
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
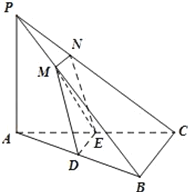
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
【答案】(1)证明见解析(2)不存在,详见解析(3)存在,证明见解析
【解析】
(1)![]() ,直角梯形
,直角梯形![]() 的两底长度
的两底长度![]() ,
,![]() .高为
.高为![]() ,利用梯形面积公式表示出
,利用梯形面积公式表示出![]() .利用等比数列定义进行证明即可;
.利用等比数列定义进行证明即可;
(2)![]() ,
,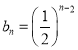 ,以
,以![]() ,
,![]() ,
,![]() 为边长能构成一个三角形,则
为边长能构成一个三角形,则![]() 考查不等式解的情况作解答;
考查不等式解的情况作解答;
(3)利用无穷等比数列求和公式,将![]() 化简为
化简为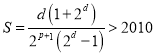 ,则
,则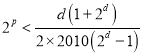 ,探讨p的存在性.
,探讨p的存在性.
解:(1)![]() ,
,![]() ,
,
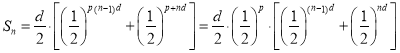 ,
,
对于任意自然数n,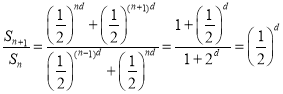 ,
,
所以数列![]() 是等比数列且公比
是等比数列且公比![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(2)![]() ,
,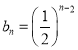 ,
,
对每个正整数![]() ,
,![]() ,
,
若以![]() ,
,![]() ,
,![]() 为边长能构成一个三角形,
为边长能构成一个三角形,
则![]() ,即
,即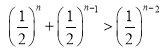 ,
,
即有![]() ,这是不可能的.
,这是不可能的.
所以对每一个正整数![]() ,以
,以![]() ,
,![]() ,
,![]() 为边长不能构成三角形;
为边长不能构成三角形;
(3)由(1)知,![]() ,
,![]() ,
,
所以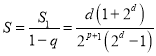 ,
,
若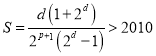 ,则
,则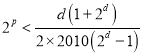
两边取对数,知只要![]() 取值为小于
取值为小于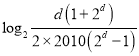 的实数,
的实数,
就有![]() .
.

练习册系列答案
相关题目