Question

【题目】已知集合M是具有下列性质的函数的全体:存在实数对,使得对定义域内任意实数x都成立.

（1）判断函数,是否属于集合;

（2）若函数具有反函数,是否存在相同的实数对,使得与同时属于集合若存在,求出相应的;若不存在,说明理由;

（3）若定义域为的函数属于集合,且存在满足有序实数对和;当时,的值域为,求当时函数的值域.

Answer 1

【答案】（1）（2）不存在实数对,使得与同时属于集合M.见解析（3）

【解析】

（1）根据已知中集合的定义,分别判断两个函数是否满足条件,即可求得答案;

（2）假定,求出相应的值,得到矛盾,即可求得答案;

（3）利用题中的新定义,列出两个等式恒成立;将x用代替,两等式结合得到函数值的递推关系;用不完全归纳的方法求出值域.

（1）当时,

,其值不为常数,

故,

当时,,

当时,,

故存在实数对,使得对定义域内任意实数x都成立,

故;

（2）若函数具有反函数,且,

则,

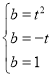则,解得:,

此时,不存在反函数,

故不存在实数对,使得与同时属于集合M.

（3）函数,且存在满足条件的有序实数对和,

于是,,

用替换中得:,

当时,,,

时,.

又由得:,

故,即,

可得:.

时,,

时,,

……

依此类推可知时,,

故时,,

综上所述,时,,

时,,

综上所述,当时函数的值域为.