Question

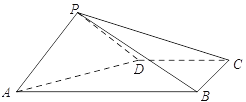
【题目】(2016·广州模拟)如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1，∠BAC＝120°，D，D1分别是线段BC，B1C1的中点，过线段AD的中点P作BC的平行线，分别交AB，AC于点M，N.

(1)证明：MN⊥平面ADD1A1；

(2)求二面角A－A1M－N的余弦值．

Answer 1

【答案】（1）详见解析；（2）.

【解析】试题分析：（1）要证线面垂直，就要证线线垂直，即要证与平面内两条相交直线垂直，首先由三棱柱侧棱与底面垂直可得，由等腰三角形性质知，从而有，因此即证线面垂直；（2）要求二面角，关键是作出二面角的平面角，一般要找到二面角的一个面的垂线，则平面角易作，因此我们连接，作于，由（1）可证平面，根据三垂线定理可得所求二面角的平面角，并在相应直角三角形中可求得此角大小.

试题解析：(1)因为AB＝AC，D是BC的中点，

所以BC⊥AD.

由题可知MN∥BC，

所以MN⊥AD.

因为AA1⊥平面ABC，MN平面ABC，

所以AA1⊥MN.

又AD，AA1在平面ADD1A1内，且AD与AA1相交于点A，

所以MN⊥平面ADD1A1.

(2)解　如图，连结A1P，过点A作AE⊥A1P于点E，过点E作EF⊥A1M于点F，连结AF.

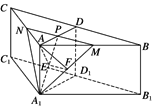
由(1)知，MN⊥平面AEA1，

所以平面AEA1⊥平面A1MN.

因为平面AEA1∩平面A1MN＝A1P，AE⊥A1P，AE平面AEA1，

所以AE⊥平面A1MN，则A1M⊥AE，又AE∩EF＝E，

所以A1M⊥平面AEF，则A1M⊥AF，

故∠AFE为二面角A－A1M－N的平面角(设为θ)．

设AA1＝1，则由AB＝AC＝2AA1，∠BAC＝120°，

D为BC的中点，有∠BAD＝60°，AB＝2，AD＝1.

又P为AD的中点，M为AB的中点，

所以AP＝，AM＝1.

在Rt△AA1P中，A1P＝，

在Rt△A1AM中，A1M＝，

从而AE＝，

AF＝，

所以sinθ＝.

因为∠AFE为锐角，

所以.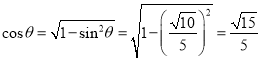

故二面角A－A1M－N的余弦值为.