题目内容
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面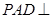 底面
底面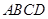 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形,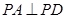 ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
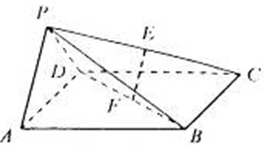
(1)求证:EF//平面PAD;
(2)求证:平面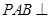 平面
平面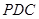 .
.
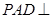 底面
底面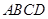 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形,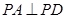 ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
(1)求证:EF//平面PAD;
(2)求证:平面
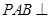 平面
平面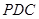 .
.详见解析
试题分析:(1)要证
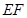 //平面
//平面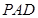 ,可证明
,可证明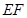 与平面
与平面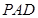 内的一条直线平行,边结
内的一条直线平行,边结 由中位线定理得这条直线就是
由中位线定理得这条直线就是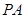 .(2)利用面面垂直的性质可由面面垂直(侧面
.(2)利用面面垂直的性质可由面面垂直(侧面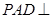 底面)得线面垂直(
底面)得线面垂直(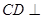 平面
平面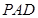 ),进而得到线线垂直(
),进而得到线线垂直(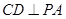 ),再结合线线垂直
),再结合线线垂直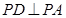 ,又得到线面垂直
,又得到线面垂直 平面
平面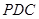 ,证明.平面
,证明.平面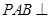 平面
平面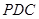 可通过
可通过 平面
平面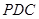 证明.
证明.试题解析:(1)证明:连接
 ,
,因为
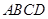 是正方形,
是正方形,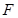 为
为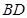 的中点,所以
的中点,所以 过点
过点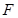 ,且
,且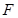 也是
也是 的中点,
的中点,因为
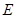 是
是 的中点,所以
的中点,所以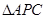 中,
中,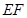 是中位线,所以
是中位线,所以
因为
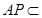 平面
平面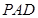 ,
,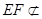 平面
平面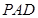 ,所以
,所以 平面
平面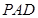
(2)因为侧面
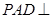 底面
底面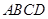 ,
,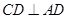
所以
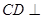 平面
平面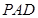
所以
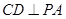
又因为
 ,
,所以
 平面
平面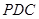 ,
,因为
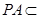 平面
平面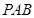 ,
,所以面
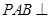 平面
平面

练习册系列答案
相关题目
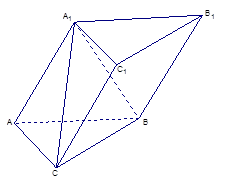
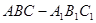 中,四边形
中,四边形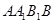 是菱形,四边形
是菱形,四边形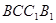 是矩形,
是矩形, .
.
 ;
; 到平面
到平面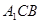 的距离;
的距离;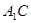 与平面
与平面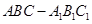 中,点
中,点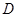 是
是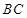 上一点.
上一点.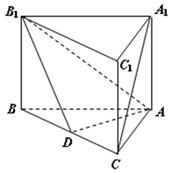
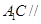 平面
平面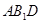 ;
;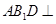 平面
平面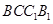 ,求证
,求证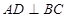 .
.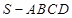 中, 底面四边形
中, 底面四边形 是直角梯形,
是直角梯形, 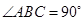 ,
,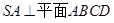 ,
,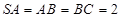 .
.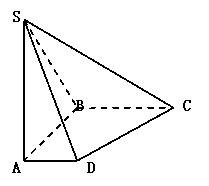
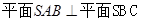 ;
; 与底面
与底面 所在的平面与正方形
所在的平面与正方形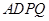 所在的平面相互垂直,
所在的平面相互垂直,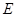 是
是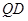 的中点.
的中点.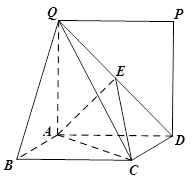
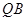 ∥平面
∥平面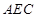 ;
;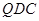 ⊥平面
⊥平面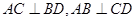 ,则
,则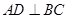 ;
;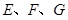 分别是
分别是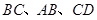 的中点,则
的中点,则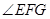 的大小等于异面直线
的大小等于异面直线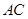 与
与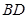 所成角的大小;
所成角的大小;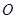 是四面体
是四面体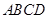 外接球的球心,则
外接球的球心,则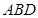 上的射影为
上的射影为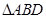 的外心;
的外心; 为两条直线,
为两条直线, 为两个平面,下列四个命题中正确的是
为两个平面,下列四个命题中正确的是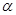 所成的角相等,则
所成的角相等,则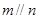
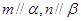 ,
,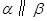 ,则
,则 ,则
,则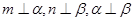 ,则
,则
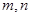 与平面
与平面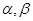 ,给出下列三个结论:①若
,给出下列三个结论:①若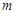 ∥
∥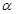 ,
,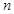 ∥
∥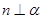 ,则
,则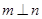 ; ③若
; ③若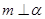 ,
,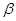 ,则
,则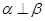 .
.