题目内容
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
【答案】(1)an=2n(2)10
【解析】
(1)由数列{an}的前n项和与项满足Sn+2=2an,n∈N*.消掉Sn可得数列{an}是等比数列,进而求数列{an}的通项公式.
(2)由(1)得数列{bn}的通项公式,裂项求和算出Tn=1![]() ,再由Tn
,再由Tn![]() ,解整数不等式可求n的最小值.
,解整数不等式可求n的最小值.
(1)当n=1时,S1+2=2a1,解得a1=2,
当n≥2时,Sn﹣1+2=2an﹣1,∴Sn+2﹣(Sn﹣1+2)=2an﹣2an﹣1,即an=2an﹣1
∴![]() 2,则{an}是以2为首项,2为公比的等比数列.
2,则{an}是以2为首项,2为公比的等比数列.
故an=2n.
(2)由(1)可得bn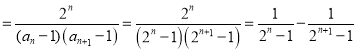
∴Tn=b1+b2+…+bn=(1![]() )+(
)+(![]() )+…+(
)+…+(![]() )=1
)=1![]() ,
,
又Tn![]() ,即1
,即1![]() ,
,
∴2n+1>2021,由于n∈N,∴n≥10,
故n的最小值为10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目