Question

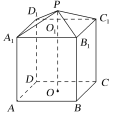
【题目】现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P－A1B1C1D1，下部的形状是正四棱柱ABCD－A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍，若AB＝6 m，PO1＝2 m，则仓库的容积是多少？

Answer 1

【答案】

【解析】

分别计算四棱锥和四棱柱的体积，相加即得．

由PO1＝2 m，知O1O＝4PO1＝8 m.因为A1B1＝AB＝6 m，所以正四棱锥P－A1B1C1D1的体积V锥＝··PO1＝×62×2＝24(m3)；

正四棱柱ABCD－A1B1C1D1的体积

V柱＝AB2·O1O＝62×8＝288(m3)，

所以仓库的容积V＝V锥＋V柱＝24＋288＝312(m3).

故仓库的容积是312 m3.