题目内容
【题目】在三棱锥![]() 中,
中,![]() .
.

(1)求证:![]() ;
;
(2)若点![]() 为
为![]() 上一点,且
上一点,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点E,连接
的中点E,连接![]() ,然后由等腰三角形的性质推出
,然后由等腰三角形的性质推出![]() ,从而利用线面垂直的判定定理与性质可使问题得证;
,从而利用线面垂直的判定定理与性质可使问题得证;
(2)以![]() 为坐标原点建立空间直角坐标系,然后求出相关点的坐标,再求出平面
为坐标原点建立空间直角坐标系,然后求出相关点的坐标,再求出平面![]() 的一个法向量,从而利用空间向量的夹角公式求解即可.
的一个法向量,从而利用空间向量的夹角公式求解即可.
解: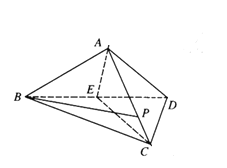
(1)证明:取![]() 的中点E,连接
的中点E,连接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
同理可得![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)∵![]() ,
,
∴![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
又![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() ,
,
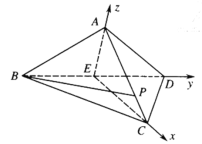
∴以![]() 为坐标原点,
为坐标原点,![]() 所在直线为x轴,
所在直线为x轴,![]() 所在直线为y轴,
所在直线为y轴,![]() 所在直线为z轴建立如图所示的空间直角坐标系.
所在直线为z轴建立如图所示的空间直角坐标系.
∴![]() ,
,
设![]() ,∵
,∵![]() ,
,![]() ,
,
∴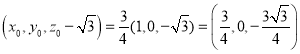 ,
,
∴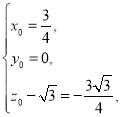 ∴
∴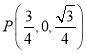 ,
,
∴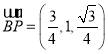 ,
,
又![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则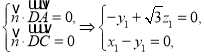
令![]() ,得
,得![]() ,∴
,∴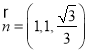 ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则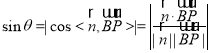
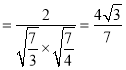 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)