题目内容
设函数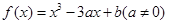 .
.
(1)若曲线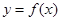 在点
在点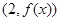 处与直线
处与直线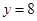 相切,求
相切,求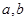 的值;
的值;
(2)求函数 的单调区间与极值点.
的单调区间与极值点.
(3)设函数 的导函数是
的导函数是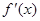 ,当
,当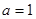 时求证:对任意
时求证:对任意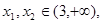
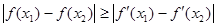 成立
成立
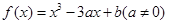 .
.(1)若曲线
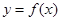 在点
在点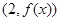 处与直线
处与直线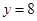 相切,求
相切,求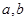 的值;
的值;(2)求函数
 的单调区间与极值点.
的单调区间与极值点.(3)设函数
 的导函数是
的导函数是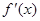 ,当
,当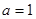 时求证:对任意
时求证:对任意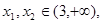
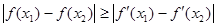 成立
成立(1)a=4,b=24
(2)当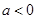 时,
时,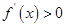 ,函数
,函数 在
在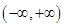 上单调递增,此时函数
上单调递增,此时函数 没有极值点
没有极值点
当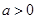 时,由
时,由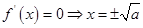 ,此时
,此时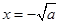 是
是 的极大值点,
的极大值点,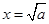 是
是 的极小值点.
的极小值点.
(3)根据由(2)知 在
在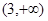 上单调递增,又
上单调递增,又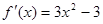 在
在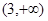 上也单调递增,函数单调性来证明不等式
上也单调递增,函数单调性来证明不等式
(2)当
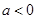 时,
时,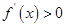 ,函数
,函数 在
在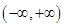 上单调递增,此时函数
上单调递增,此时函数 没有极值点
没有极值点当
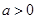 时,由
时,由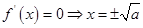 ,此时
,此时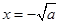 是
是 的极大值点,
的极大值点,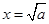 是
是 的极小值点.
的极小值点.(3)根据由(2)知
 在
在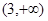 上单调递增,又
上单调递增,又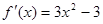 在
在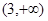 上也单调递增,函数单调性来证明不等式
上也单调递增,函数单调性来证明不等式试题分析:解.(1)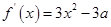 ,
,
∵曲线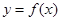 在点
在点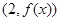 处与直线
处与直线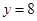 相切,
相切,
∴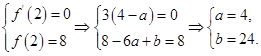
(2)∵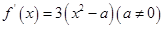 ,
,
当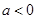 时,
时,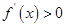 ,函数
,函数 在
在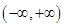 上单调递增,
上单调递增,
此时函数 没有极值点.
没有极值点.
当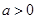 时,由
时,由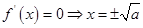 ,
,
当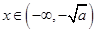 时,
时,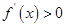 ,函数
,函数 单调递增,
单调递增,
当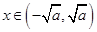 时,
时,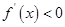 ,函数
,函数 单调递减,
单调递减,
当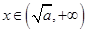 时,
时,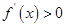 ,函数
,函数 单调递增,
单调递增,
∴此时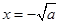 是
是 的极大值点,
的极大值点,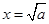 是
是 的极小值点.
的极小值点.
(3)不妨设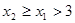 ,因为
,因为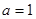 由(2)知
由(2)知 在
在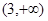 上单调递增,
上单调递增,
又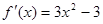 在
在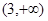 上也单调递增,
上也单调递增,
所以要证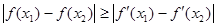
只需证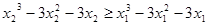
设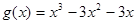 ,
,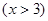
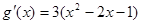 ,
,
当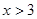 时,
时,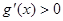 ,
,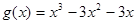 在
在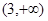 上单调递增
上单调递增
所以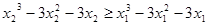 成立
成立
所以对任意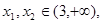
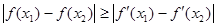 成立
成立
点评:主要是考查了导数研究函数单调性的运用,以及证明不等式,属于难度题。
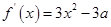 ,
,∵曲线
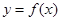 在点
在点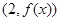 处与直线
处与直线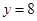 相切,
相切,∴
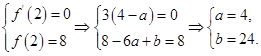
(2)∵
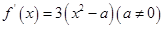 ,
,当
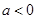 时,
时,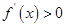 ,函数
,函数 在
在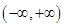 上单调递增,
上单调递增,此时函数
 没有极值点.
没有极值点.当
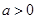 时,由
时,由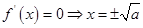 ,
,当
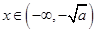 时,
时,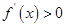 ,函数
,函数 单调递增,
单调递增,当
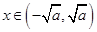 时,
时,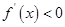 ,函数
,函数 单调递减,
单调递减,当
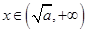 时,
时,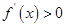 ,函数
,函数 单调递增,
单调递增,∴此时
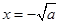 是
是 的极大值点,
的极大值点,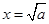 是
是 的极小值点.
的极小值点.(3)不妨设
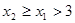 ,因为
,因为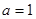 由(2)知
由(2)知 在
在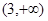 上单调递增,
上单调递增,又
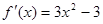 在
在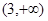 上也单调递增,
上也单调递增,所以要证
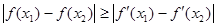
只需证
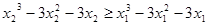
设
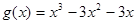 ,
,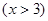
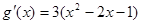 ,
,当
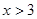 时,
时,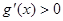 ,
,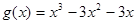 在
在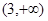 上单调递增
上单调递增所以
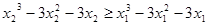 成立
成立所以对任意
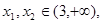
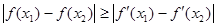 成立
成立点评:主要是考查了导数研究函数单调性的运用,以及证明不等式,属于难度题。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
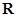 上的偶函数
上的偶函数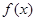 满足:对任意
满足:对任意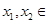 [0,+∞),且
[0,+∞),且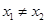 都有
都有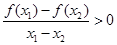 ,则( )
,则( )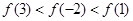
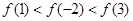
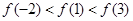
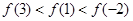
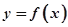 与
与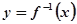 互为反函数,且函数
互为反函数,且函数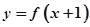 与函数
与函数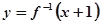 也互为反函数,若
也互为反函数,若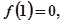 则
则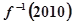 =( )
=( )
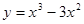 在
在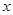 等于 处取得极小值.
等于 处取得极小值.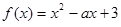 在(0,1)上为减函数,函数
在(0,1)上为减函数,函数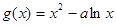 的(1,2)上为增函数,则a的值等于
的(1,2)上为增函数,则a的值等于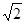
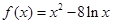 ,
,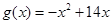 .
.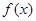 在点
在点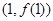 处的切线方程;
处的切线方程;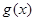 在区间
在区间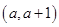 上均为增函数,求
上均为增函数,求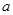 的取值范围;
的取值范围;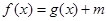 有唯一解,试求实数
有唯一解,试求实数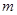 的值.
的值. 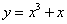 的递增区间是( )
的递增区间是( )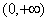
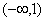
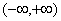
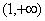
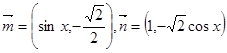 ,函数
,函数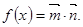
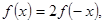 求
求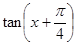 的值;
的值;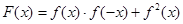 的最大值和单调递增区间。
的最大值和单调递增区间。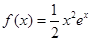 .
.