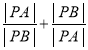Question

【题目】已知点，过点D作抛物线的切线l，切点A在第二象限．

（1）求切点A的纵坐标．

（2）有一离心率为的椭圆恰好经过切点A，设切线l与椭圆的另一交点为点B，切线l，的斜率分别为，若成等差数列，求椭圆的方程．

Answer 1

【答案】（1）纵坐标；（2）.

【解析】

（1）利用导数的几何意义求出切线的方程，点D 的坐标代入切线方程可得，再由点A在抛物线上有，得解；（2）由椭圆的离心率得，代入椭圆方程并与直线的方程联立得关于x的一元二次方程，利用韦达定理用k、b表示出、，由成等差数列可得，由已知条件将上式转化为关于k、b的方程即可求得b，从而求得椭圆方程.

（1）设切点，则有，

，，由切线l的斜率为，得l的方程为，

又点在l上，所以，即，所以点A的纵坐标．

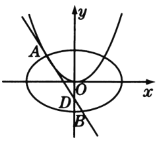
（2）由（1）得，切线斜率，

设，切线方程为，

由得，

又，所以，所以椭圆方程为．

由得，，．

又因为成等差数列，所以，

即

，

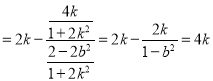解得，所以，所以椭圆方程为．