题目内容
已知函数 在区间
在区间 上单调递减,则
上单调递减,则 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
D
解析试题分析:∵f(x)=ax-x3, ∴f′(x)=a-3x2∵函数f(x)=ax-x3在区间[1,+∞)上单调递减,∴f′(x)=a-3x2≤0在区间[1,+∞)上恒成立,
∴a≤3x2在区间[1,+∞)上恒成立,∴a≤3.故选D.
考点:运用导数研究函数的单调性及恒成立问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列四个判断:
①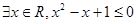 ;
;
②已知随机变量X服从正态分布N(3, ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28;
③已知 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;
④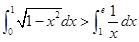
其中正确的个数有:
| A.1个 | B.2个 | C.3个 | D.4个 |
函数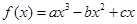 的图象如图所示,且
的图象如图所示,且 在
在 与
与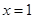 处取得极值,给出下列判断:
处取得极值,给出下列判断: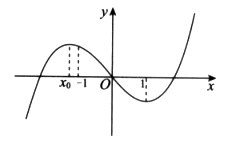
①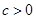 ;
;
②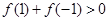 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
定义在R上的函数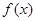 满足
满足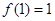 ,且对任意
,且对任意 都有
都有 ,则不等式
,则不等式 的解集为( )
的解集为( )
| A.(1,2) | B.(0,1) | C.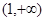 | D.(-1,1) |
若f(x)=x2-2x-4ln x,则f′(x)>0的解集为( )
| A.(0,+∞) | B.(-1,0)∪(2,+∞) |
| C.(2,+∞) | D.(-1,0) |
若函数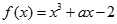 在区间
在区间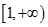 内是增函数,则实数
内是增函数,则实数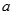 的取值范围是( )
的取值范围是( )
A.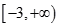 | B.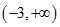 | C.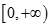 | D.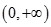 |
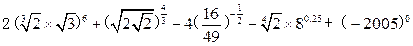
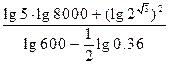 。
。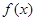 的定义域为开区间
的定义域为开区间 ,其导函数
,其导函数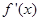 在
在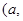
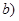 内极小值点的个数为( )
内极小值点的个数为( )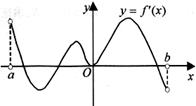
 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: 均有
均有 成立;
成立;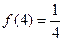 ;
; 时,都有
时,都有 成立。
成立。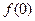 ,
, 的值;
的值; 的不等式
的不等式 .
.