题目内容
【题目】设椭圆
的一个顶点与抛物线
的焦点重合，
，
分别是椭圆
的左、右焦点，离心率
，过椭圆右焦点的直线
与椭圆交于
，
两点．
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在直线，使得
，若存在，求出直线的方程；若不存在，说明理由；
（Ⅲ）设点
是一个动点，若直线的斜率存在，且
为
中点，
，求实数
的取值范围．
【答案】(Ⅰ)
；(Ⅱ)答案见解析；(Ⅲ)
.
【解析】
(Ⅰ)由题意求得a,b,c的值即可确定椭圆方程；
(Ⅱ)联立直线方程与椭圆方程，结合韦达定理和向量的坐标运算法则求得直线的斜率即可确定直线方程；
(Ⅲ)由题意结合点差法得到
的表达式，结合其表达式求解取值范围即可.
(Ⅰ)抛物线
的焦点坐标为
，故
，
结合
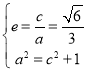可得：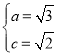
，故椭圆方程为：.
(Ⅱ)很明显直线的斜率存在，设
，
假设存在满足题意的直线方程：
，
与椭圆方程联立可得：
，
则
，
则：
，
结合题意和韦达定理有：
，
解得：
，即存在满足题意的直线方程：
.
(Ⅲ)设
，设直线AB的方程为
，
由于：
，
两式作差整理变形可得：
，
即：
. ①
又
②
③
①×②可得：
④
④代入③可得：
⑤
④⑤代入①整理可得：
，
，据此可得：
，
从而.
练习册系列答案
相关题目
